Вот, собственно. Интересует, как его посчитать ручками (mathcad-ом пользоваться умею).

Спасибо.

Это табличный интеграл - используется вроде в теории статистической РТС. В частности для расчета вероятности ошибочно приема.

Сей интеграл будет табличным, если верхний предел - переменная величина.
Называется - интеграл вероятности.
Если пределы таковы, как указано в посте - то значение определено и равно
SQRT( PI/2 ) ( извините, формулы вставлять не умею.....)

См.: Двайт "Таблицы интегралов и другие ..."

Точно. Еще раз большое спасибо.

Пардон, поправлю, это т.н. интеграл Пуассона, обычно есть в учебниках по матанализу, где я его и посмотрел.
Однако, пишут что SQRT(pi)/2.

У вышеуказанного Двайта приведено: интеграл(exp(-r^2*x^2) равен SQRT(pi)/2/r.
Мне кажется, что в нашем случае r=1/SQRT(2).

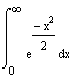Вот без двойки в знаменателе для простоты. Домножим искомый интеграл на такое же выражение, где вместо x стоит y. Получится квадрат искомого. Поглядим на то, что получилось в полярных координатах.
Интеграл от r^2 по dS. Перепишем dS в виде 2*pi*r*dr*dfi. Получившийся интеграл по плоскости будет равен 2pi. Осталось извлечь корень. Жульничество, конечно...Корректность оставляет желать... Но ответ правильный.

Извиняюсь, ошибочка вышла, вчера я двойку в знаменателе не заметил.

И у меня ошибка - показалось что от - бесконечности до + бесконечности. Поэтому ответ в четыре раза больше. Когда пишешь ответ, формула не видна.... И еще описка 2*pi получается уже после интегрирования по углу. Поэтому dfi уже не нужно. dS=dx*dy=r*dr*dfi=2*pi*r*dr

Сообщение отредактировал Tanya - Jun 23 2006, 05:57

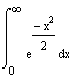вот тут вывод, если интересно, все без жульничества
http://www.students.chemport.ru/materials/matan/m4/l3.pdf
в итоге получится sqrt(2pi)/2

Это то самое жульничество - отсутствует доказательство того, что произведение интегралов сводится к интегралу по плоскости, хотя это интуитивно ясно.

Смотрите курс математического анализа, раздел "Сведение кратного интеграла к повторному"

В разных курсах разная степень сторогости. Даже определение определенного интеграла для функции одного переменного (напр. как предел сумм Дарбу) и интегралов функций n переменных отличается...