| |
|
  |
 Вопросы по итеративному декодированию Вопросы по итеративному декодированию, Реализация CTC/BTC/LDPC кодов |
|
|
|
|
 Mar 26 2015, 09:53 Mar 26 2015, 09:53
|
Знающий
   
Группа: Участник
Сообщений: 527
Регистрация: 4-06-14
Из: Санкт-Петербург
Пользователь №: 81 866

|
Цитата проверка sum(abs(rx_symb - tx_symb).^2)/Nbits и sum(abs(rx_symb1 - tx_symb1).^2)/Nbits показывает что мощность шума у вас там разная. Точно. Нужно немного поправить, во первых я неправильно взвешивал шум, нужно так: Код noise = randn(1, Nbits)+1j*randn(1, Nbits);
noise = noise * sqrt(Pn/2); А во-вторых: Код rx_symb = tx_symb + noise;
rx_symb1 = tx_symb1 + noise; Даёт результат: Код ber = 0.022872 ber1 = 0.023012 и Код >> sum(abs(rx_symb - tx_symb).^2)/Nbits
ans =
1.0017
>> sum(abs(rx_symb1 - tx_symb1).^2)/Nbits
ans =
1.0017 В таком случае действительный сигнал tx_symb1 трактуется как комплексный с im=0. Но вот другой интересный эффект заметил: Формально, т.к. оба сигнала теперь считаются комплексными к ним должно применяться одно правило принятия решений: Код hd_bits = ((real(rx_symb) + imag(rx_symb)) >= 0);
hd_bits1 = ((real(rx_symb1) + 1*imag(rx_symb1)) >= 0); Но тогда получается Код ber = 0.023051 ber1 = 0.079219 А если второе созвездие предварительно развернуть: Код rx_symb1 = rx_symb1 * exp(1i*pi/4); то получается Код ber = 0.02295 ber1 = 0.0228 Как же так? Кажется нашел ответ на свой вопрос: правило Код hd_bits = ((real(rx_symb) + imag(rx_symb)) >= 0); Даёт лучший результат при 100% восстановленной фазе, т.е. при когерентном приёме, а в остальных случаях получаются потери вплоть до 3дБ, что соответствует некогерентному приёму. Так ли это?
|
|
|
|
|
|
|
|
 Mar 26 2015, 09:53 Mar 26 2015, 09:53
|
Вечный ламер
     
Группа: Модераторы
Сообщений: 7 248
Регистрация: 18-03-05
Из: Томск
Пользователь №: 3 453

|
Цитата(serjj @ Mar 26 2015, 16:46)  Но вот другой интересный эффект заметил: Угу, я тоже его заметил. Похоже весь сыр бор вокруг вокруг вот этого Код if(strcmp(cplxMode,'complex'))
y = (sqrt(imp*noisePower/2))*(func(row, col)+1i*func(row, col));
else
y = (sqrt(imp*noisePower))*func(row, col);
end; Правда не понятно как тогда быть обработкой "разных" BPSK. Так можно на 3дб ошибиться, а потом считать свой декодер супер-пупер крутым 
--------------------
|
|
|
|
|
|
|
|
 Mar 26 2015, 10:01 Mar 26 2015, 10:01
|
Знающий
   
Группа: Свой
Сообщений: 565
Регистрация: 22-02-13
Пользователь №: 75 748

|
Цитата(serjj @ Mar 26 2015, 12:53)  Даёт лучший результат при 100% восстановленной фазе, т.е. при когерентном приёме, а в остальных случаях получаются потери вплоть до 3дБ, что соответствует некогерентному приёму. Так ли это? Это я вчера так коряво с одномерным созвездием пытался объяснить этот случай  Да, теперь нужно знать точно фазу, поскольку используются две координаты. Цитата(des00 @ Mar 26 2015, 12:53)  Правда не понятно как тогда быть обработкой "разных" BPSK. Так можно на 3дб ошибиться, а потом считать свой декодер супер-пупер крутым  Использовать Simulink, о чем я написал выше  Кстати, не пробовали использовать вместо awgn объект comm Симулинковского АБГШ? По идее там должно быть всё хорошо.
Сообщение отредактировал Grizzzly - Mar 26 2015, 10:05
|
|
|
|
|
|
|
|
 Mar 26 2015, 11:35 Mar 26 2015, 11:35
|
Знающий
   
Группа: Участник
Сообщений: 527
Регистрация: 4-06-14
Из: Санкт-Петербург
Пользователь №: 81 866

|
Цитата Правда не понятно как тогда быть обработкой "разных" BPSK. Для BPSK с произвольным поворотом на угол ang от оси Ox правило принятия решения будет: Код a = cos(degtorad(ang));
b = sin(degtorad(ang));
hd_bits1 = ((a*real(rx_symb1) + b*imag(rx_symb1)) >= 0); Это даёт BER порядка 0.023 для любых углов поворота при SNR=3 дБ.
|
|
|
|
|
|
|
|
 Mar 26 2015, 21:34 Mar 26 2015, 21:34
|
Знающий
   
Группа: Свой
Сообщений: 565
Регистрация: 22-02-13
Пользователь №: 75 748

|
Провел тщательный эксперимент.  В MATLAB pskmod для BPSK возвращает комплексные значения вида (+/-1 + j0). Поэтому awgn работает корректно. Ничего добавлять не нужно к SNR. В Simulink. Создал вместо стандартного BPSK-модулятора свой на блоках умножения на 2 и с вычитанием 1. На выходе вещественные числа. Если задаю в AWGN Eb/N0 = 3 дБ, получаю правильный BER = 0.023. Если SNR = 3 дБ, то неверный BER = 0.07. Стандартный BPSK-модулятор в Simulink также формирует комплексные значения (+/-1 + j0). Тут всегда верно. Соглашусь с serjj, лучше всегда прибавлять к сигналу 1j*1e-15, а потом брать вещественную часть. Либо уж стандартной функций pskmod пользоваться. Тогда точно никаких ошибок не будет.
Сообщение отредактировал Grizzzly - Mar 26 2015, 21:34
|
|
|
|
|
|
|
|
 Mar 27 2015, 18:09 Mar 27 2015, 18:09
|
Вечный ламер
     
Группа: Модераторы
Сообщений: 7 248
Регистрация: 18-03-05
Из: Томск
Пользователь №: 3 453

|
Всем доброго! Отложил немного турбокоды, ушел в другую сторону стандарта Wimax. Сделал в матлабе эталонную модель LDPC декодера, алгоритм декодирования Normalized Min-Sum и 2-D Normalized Min-Sum. В процессе снятия характеристик, обнаружил один, не очень понятный мне эффект. В приложении матлабовский код bertest а. В главном файле bertest.m есть параметр ERR_MODE = 0. Он может принимать значения 0/1. Режимы 0/1 отличаются инверсией символов радиоканала и битовой инверсией результатов декодирования при измерении коэффициента ошибок. Код .....
if ERR_MODE == 1
rx_symb = awgn(tx_symb, SNR, 10*log10(2));
else
rx_symb = awgn(-1*tx_symb, SNR, 10*log10(2));
end
.....
if ERR_MODE == 1
err = biterr(code(1:Nbits), decode(1:Nbits));
else
err = biterr(code(1:Nbits), not(decode(1:Nbits)));
end Так вот, качество работы декодера, в разных режимах, существенно отличается. В режиме 1 он работает намного хуже ber где то 10^-2, в режиме 0 ber нулевой. Полдня не мог понять что же сделано неправильно. Перечитывая на Nый раз статью Optimized Min-Sum Decoding Algorithm for Low Density Parity Check Codes, взгляд упал на описание алгоритма (скрин в приложении). Они в этом алгоритме инвертируют входные метрики и считают инверсные жесткие решения. Пробежался по другой литературе и во многих статьях наблюдается этот эффект. Проясните что это за эффект ? Логическое обоснование результатов, подсказывает мне что min-sum обладает чем то, вроде постоянного смещения в вычисляемых LLR, и начальная инверсия метрик является чем то вроде коррекции этого смещения. Но в турбокодах же такого нет, или просто я случайно угадал с инверсией? Спасибо. ЗЫ. Раз полез в LDPC коды, то название темы изменил на более корректное 
Эскизы прикрепленных изображений
 РЈРСВВВВВВВВеньшено Р В Р’В Р СћРІР‚ВВВВВВВР С• 69% 
544 x 734 (84.42 килобайт)
|
--------------------
|
|
|
|
|
|
|
|
 Mar 27 2015, 20:11 Mar 27 2015, 20:11
|
Местный
  
Группа: Участник
Сообщений: 453
Регистрация: 23-07-08
Пользователь №: 39 163

|
Цитата(des00 @ Mar 27 2015, 21:09)  Так вот, качество работы декодера, в разных режимах, существенно отличается. В режиме 1 он работает намного хуже ber где то 10^-2, в режиме 0 ber нулевой. Для меня (не знаток LDPC и особенно того LDPC, что в ваймакс) вовсе не очевидно, что инвертированное кодовое слово тоже является кодовым словом. По логике вещей, если с - кодовое слово, то его инверсия - это: с+ones(1, Nbits/rate). Для того, чтобы это выполнялось, слово из всех единиц должно быть кодовым. Вот и встает вопрос - выполняется ли ones * H' = 0 для рассматриваемого кода. Закодировал твоим кодером все единицы и НЕ получил кодовое слово из всех единиц, т.е. код как минимум не систематический. Сгенери полную проверочную матрицу и проверь (сумма столбцов (??? может, строк, плохо соображаю) проверочной матрицы должна быть равна zeros).
Сообщение отредактировал andyp - Mar 27 2015, 20:23
|
|
|
|
|
|
|
|
 Mar 27 2015, 20:20 Mar 27 2015, 20:20
|

я только учусь...
     
Группа: Модераторы
Сообщений: 3 447
Регистрация: 29-01-07
Из: Украина
Пользователь №: 24 839

|
Цитата(des00 @ Mar 27 2015, 20:09)  Всем доброго! Отложил немного турбокоды, ушел в другую сторону стандарта Wimax. Сделал в матлабе эталонную модель LDPC декодера, алгоритм декодирования Normalized Min-Sum и 2-D Normalized Min-Sum. В процессе снятия характеристик, обнаружил один, не очень понятный мне эффект. В приложении матлабовский код bertest а. В главном файле bertest.m есть параметр ERR_MODE = 0. Он может принимать значения 0/1. Режимы 0/1 отличаются инверсией символов радиоканала и битовой инверсией результатов декодирования при измерении коэффициента ошибок. Код .....
if ERR_MODE == 1
rx_symb = awgn(tx_symb, SNR, 10*log10(2));
else
rx_symb = awgn(-1*tx_symb, SNR, 10*log10(2));
end
.....
if ERR_MODE == 1
err = biterr(code(1:Nbits), decode(1:Nbits));
else
err = biterr(code(1:Nbits), not(decode(1:Nbits)));
end Так вот, качество работы декодера, в разных режимах, существенно отличается. В режиме 1 он работает намного хуже ber где то 10^-2, в режиме 0 ber нулевой. Полдня не мог понять что же сделано неправильно. Перечитывая на Nый раз статью Optimized Min-Sum Decoding Algorithm for Low Density Parity Check Codes, взгляд упал на описание алгоритма (скрин в приложении). Они в этом алгоритме инвертируют входные метрики и считают инверсные жесткие решения. Пробежался по другой литературе и во многих статьях наблюдается этот эффект. Проясните что это за эффект ? Логическое обоснование результатов, подсказывает мне что min-sum обладает чем то, вроде постоянного смещения в вычисляемых LLR, и начальная инверсия метрик является чем то вроде коррекции этого смещения. Но в турбокодах же такого нет, или просто я случайно угадал с инверсией? Спасибо. ЗЫ. Раз полез в LDPC коды, то название темы изменил на более корректное  но инверсия может декодеру не помочь, а наоборот ухудшить ситуацию с декодированием - не будет декодироваться. и наоборот. Лучше для каждого сигнала брать пару-тройку входных данных и пробовать их декодировать с инверсией и без инверсии - соответственно принимать решение изначально инвертировать входные данные или нет. Намного лучше декодируется 4-5 битные входные данные ("мягкие" входные данные), чем их жесткое соответствие 1/0 (бывает даже в разы)
--------------------
If it doesn't work in simulation, it won't work on the board.
"Ты живешь в своих поступках, а не в теле. Ты — это твои действия, и нет другого тебя" Антуан де Сент-Экзюпери повесть "Маленький принц"
|
|
|
|
|
|
|
|
 Mar 28 2015, 15:13 Mar 28 2015, 15:13
|
Вечный ламер
     
Группа: Модераторы
Сообщений: 7 248
Регистрация: 18-03-05
Из: Томск
Пользователь №: 3 453

|
Цитата(andyp @ Mar 28 2015, 04:11)  Для того, чтобы это выполнялось, слово из всех единиц должно быть кодовым. Вот и встает вопрос - выполняется ли ones * H' = 0 для рассматриваемого кода. Закодировал твоим кодером все единицы и НЕ получил кодовое слово из всех единиц, т.е. код как минимум не систематический. Сгенери полную проверочную матрицу и проверь (сумма столбцов (??? может, строк, плохо соображаю) проверочной матрицы должна быть равна zeros). Все чудеснее и чудеснее. Взял CML сорцы и сделал простой тест. Только параметры поставил 2304 1/2 (позже скажу зачем): Код plength = 2304;
data = ones(1, plength/2);
[H_rows, H_cols, P] = InitializeWiMaxLDPC(1/2, 2304, []);
codeword = LdpcEncode( data, H_rows, P);
%
code = '1/2';
[Hb, zf, coderate] = get_wimax_ldpc_Hb(code, plength);
code = ldpc_encode(data, Hb, zf);
disp(['cml ones = ', num2str(length(find(codeword == 1))), ' cml zeros = ', num2str(length(find(codeword == 0)))]);
disp(['my ones = ', num2str(length(find(codeword == 1))), ' my zeros = ', num2str(length(find(codeword == 0)))]);
disp(['cml vs my diff = ', num2str(sum(abs(codeword - code)))]);
E = eye(zf);
[c, t] = size(Hb);
H = zeros(c*zf, t*zf);
for row = 1:c
for col = 1:t
if Hb(row, col) >= 0
H(zf*(row-1)+1 : zf*row, zf*(col-1)+1 : zf*col) = ...
circshift(E,-1*Hb(row,col));
end
end
end
sum_of_rows = zeros(1, c);
for row = 1:c
sum_of_rows(row) = sum(H(row*zf, :)); % can check only one row per zf-by-zf
end
sum_of_cols = zeros(1, t);
for col = 1:t
sum_of_cols(col) = sum(H(:,col*zf)); % can check only one col per zf-by-zf
end
disp(['H sum rows = ', num2str(sum_of_rows)]);
disp(['H sum cols = ', num2str(sum_of_cols)]);
disp(['cml check = ', num2str(H(1,:)*codeword')]);
disp(['cml inv check = ', num2str(H(1,:)*not(codeword'))]);
disp(['my check = ', num2str(H(1,:)*codeword')]);
disp(['my inv check = ', num2str(H(1,:)*not(codeword'))]); вот результат его работы: Код cml ones = 1920 cml zeros = 384
my ones = 1920 my zeros = 384
cml vs my diff = 0
H sum rows = 6 7 7 6 6 7 6 6 7 6 6 6
H sum cols = 3 3 6 3 3 6 3 6 3 6 3 6 3 2 2 2 2 2 2 2 2 2 2 2
cml check = 6
cml inv check = 0
my check = 6
my inv check = 0 1/2 2304 взял по причине того, что нашел в книге рисунок матрицы такого кода. Он в приложении. Приведу первую строку и первый столбец проверочной матрицы: Код find(H(1,:)) = 191 266 824 948 1160 1249
find(H(:,1))' = 324 853 1110 Совсем не то что приведено в книге, в других книгах точно такой же рисунок (похоже списывали друг у друга). Вот как то у меня теперь шаблон линейных кодов немного взрывается, после результатов Цитата(Maverick @ Mar 28 2015, 04:20)  но инверсия может декодеру не помочь.... в обсуждаемом коде мягкое решение без квантования. Инверсия в канале это поворот созвездия QPSK на 180 градусов. Цитата(des00 @ Mar 28 2015, 22:51)  Вот как то у меня теперь шаблон линейных кодов немного взрывается, после результатов Залез в сорцы CML, кодируют они так Код for (i=0;i<kldpc;i++){
c_in[i]=u[i]; // my: systematic bits
}
for (i=0;i<mldpc;i++){
c_in[kldpc+i]=0; // my: parity bits
}
sum=0;
for(i=0;i<mldpc;i++){ // my: mldpc - parity bit length
for(k=1;k<=wid_Hrows;k++){ // my: wid_Hrows - H rows number
if(H_rows[i+mldpc*(k-1)]!=0){
count=(int)H_rows[i+mldpc*(k-1)];
x[i]=((int)c_in[count-1])^((int)x[i]);
}
}
c_in[kldpc+i]=x[i]^sum; /* Differential encoding */
sum=c_in[kldpc+i];
} Ничего неожиданного, классический расчет битов четности, а нули в потоке образуются похоже в тех рядах где 7 единиц  UPD. Шаблон разрывает по причине того, что не могу понять почему проверка проходит на инверсных битах.
Эскизы прикрепленных изображений
 РЈРСВВВВВВВВеньшено Р В Р’В Р СћРІР‚ВВВВВВВР С• 77% 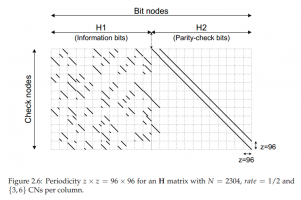
744 x 493 (76.09 килобайт)
|
--------------------
|
|
|
|
|
|
|
|
 Mar 28 2015, 17:55 Mar 28 2015, 17:55
|
Вечный ламер
     
Группа: Модераторы
Сообщений: 7 248
Регистрация: 18-03-05
Из: Томск
Пользователь №: 3 453

|
Цитата(des00 @ Mar 28 2015, 23:13)  UPD. Шаблон разрывает по причине того, что не могу понять почему проверка проходит на инверсных битах. Отвечаю сам себе. Потому что кто-то(ну т.е. я) лошпет  1. Математика там должна быть по модулю 2. 2. Проверять надо весь вектор, а не один бит. Правильный код проверки Код check = mod(H*codeword', 2);
inv_check = mod(H*not(codeword'), 2);
disp(['cml check = ', num2str(sum(check))]);
disp(['cml inv check = ', num2str(sum(inv_check))]);
check = mod(H*code', 2);
inv_check = mod(H*not(code'), 2);
disp(['my check = ', num2str(sum(check))]);
disp(['my inv check = ', num2str(sum(inv_check))]); и результат Код cml ones = 1920 cml zeros = 384
my ones = 1920 my zeros = 384
cml vs my diff = 0
H sum rows = 6 7 7 6 6 7 6 6 7 6 6 6
H sum cols = 3 3 6 3 3 6 3 6 3 6 3 6 3 2 2 2 2 2 2 2 2 2 2 2
cml check = 0
cml inv check = 384
my check = 0
my inv check = 384 т.е. все работает правильно. Это возвращает к первоначальному вопросу из поста №142: Почему декодер, в котором инвертированы метрики (умножены на -1) и декодируются инверсные биты работает лучше. Ну и на скрине статьи указано что делать нужно так 
--------------------
|
|
|
|
|
|
|
|
 Mar 28 2015, 21:03 Mar 28 2015, 21:03
|
Местный
  
Группа: Участник
Сообщений: 453
Регистрация: 23-07-08
Пользователь №: 39 163

|
Цитата(des00 @ Mar 28 2015, 20:55)  Почему декодер, в котором инвертированы метрики (умножены на -1) и декодируются инверсные биты работает лучше. Ну и на скрине статьи указано что делать нужно так  Если ты правильно сформировал матрицу (а похоже, что это так), то вектор-столбец, являющийся суммой по модулю два столбцов проверочной матрицы выглядит так - см картинку Он явно не нулевой, а это означает, что декодер будет работать по разному, в зависимости от знаков входных данных Теперь по статье. Разберемся с работой чек ноды в LDPC декодере. Пусть мы имеем простейшую чек-ноду с двумя входами, между которыми вычисляется xor, чтобы получить значение чек-бита. В этом случае, чек бит равен единице, если входы разные и 0, если они одинаковые. Для вероятностей получаем: p_c(1) = p_1(1) * p_2(0) + p_1(0) * p_2(1); p_c(0) = p_1(1) * p_2(1) + p_1(0) * p_2(0); Рассмотрим отношение p_c(1)/p_c(0). Разделим числитель и знаметатель на p_1(0) * p_2(0) и получим: p_c(1)/p_c(0) = (exp(L1) + exp(L2))/(1+exp(L1)*exp(L2)) L1, L2 - LLR первого и второго битов. p_1(1)/p_1(0) = exp(L1); p_2(1)/p_2(0) = exp(L2) Далее, используем следующее соотношение: exp(L) = (1+tanh(L/2))/(1-tanh(L/2)) - это собственно следует из определения tanh После подстановки и скучного приведения слагаемых получаем p_c(1)/p_c(0) = (1- tanh(L1/2)*tanh(L2/2))/(1 + tanh(L1/2)*tanh(L2/2)) О волшебство! получили инверсию того, что используется для чек-ноды в статье. Следовательно, в статье для чек-нод получают инверсное соотношение p_c(0)/p_c(1) Для "взрослого" случая из n входных бит чек-ноды, можно воспользоваться мат. индукцией и прийти к такому же выводу. Для variable node соотношения будут иметь тот же вид, что и в статье, но делаем вывод, что декодер работает в терминах инверсных LLR (ln(p(0)/p(1))). Именно из-за этого и инвертируют входные LLR. Если ты используешь инверсный маппинг, то получаешь инверсные LLR и твой декодер начинает работать правильно. Как-то так.
Сообщение отредактировал andyp - Mar 28 2015, 21:47
Эскизы прикрепленных изображений
 РЈРСВВВВВВВВеньшено Р В Р’В Р СћРІР‚ВВВВВВВР С• 69% 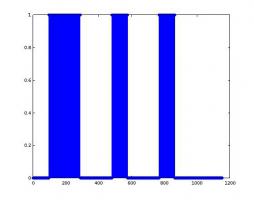
560 x 440 (17.44 килобайт)
|
|
|
|
|
|
|
|
  |
1 чел. читают эту тему (гостей: 1, скрытых пользователей: 0)
Пользователей: 0

|
|
|