Доброго дня всем!

Возможно щас глупость спрошу, но мучает один вопрос, есть приемник с двумя ПЧ (двумя преобразованиями) на первую ПЧ генератор формирует сигнал с уровнем фазовых шумов -50 дБн на вторую генератор формирует сигнал с уровнем фазовых шумов -70 дБн... Какой уровень фазовых шумов получится в итоге?

Можно еще так вопрос задать есть структурная схема приемного тракта, как на него рассчитать уровень фазовых шумов?
может есть книжки? статьи? что нибудь? или кто нить знает как правильно рассчитать?

Разобрался)

И снова здравствуйте!)

есть такой вопрос

в книжке Mohamed K. Nezami "RF Architectures and Digital Signal Processing Aspects of Digital Wireless Transceivers" в разделе 10 на стр.21 приведена
формула ухудшения ОСШ в зависимости от фазового шума и приведены графики для различных ОСШ
формула какая то такая:

и картинка уже рассчитанная мной по этой формуле вот:


Глядя на картинку для исходного ОСШ сигнала равного 20 дБ видим, что ухудшение будет в 1 дБ при fph/df = 10^-3
df судя по описанию в книге это расстояние между поднесущими, пусть это будет к примеру 50 Гц
получается ширина полосы фазового шума fph = df*10^-3 = 50*10^-3 т.е. для генератора 30 МГц это стабильность где-то 10^-9 требуется
я же правильно все посчитал? Но на практике то это не так, теория приведенная в литературе вводит нас в заблуждение, или я что то упустил?
много литературы посвящено проблеме фазовых шумов их моделированию и т.п. но проблемы то нет, как мы выяснили ранее... Да у реальных генераторов уровень фазовых шумов на несущей -60 дБ и ниже(поэтому они не могут так существенно ухудшать ОСШ т.к. находятся глубоко под шумами) и при ширине фазового шума fph=50*10^-3 ну никак не получится ухудшение в 1дБ, и тогда возникает следующий вопрос фазовый шум и нестабильность частоты это ведь одно и тоже? Тогда если взять модель генератора которая имеет профиль с 0дБ на несущей с шириной 50*10^-3Гц и далее по -20дб на декаду, то мы будем иметь что то типо дрожания(нестабильности) частоты которая известна на практике.
Тогда почему в той же книге Nezami формула ухудшения для частотного сдвига отличается от формулы приведенной для фазовых:


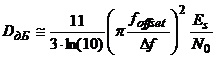
Много непонятных моментов которые я не могу уложить у себя в голове, вернее ничего непонятно
мне кажется формула ухудшения ОСШ в зависимости от фазовых шумов не верна из за того что не учитывает уровень фазовых шумов, на практике большее вилияние оказывает доплер и нестабильность частоты генератора, проблемы фазы я не вижу... но в теории она почему то раздута

Сообщение отредактировал Ivan55 - Jan 24 2017, 12:08