Есть датчик, с которого снимается сигнал. Этот сигнал фильтруется (гифка прилагается), а затем осущетвляется поиск минимума для определения периодики процесса. Сигнал далек от идеального, поэтому нужен наиболее эффективный алгоритм поиска миимума. Суть вопроса сводится к следующему - нет ли в свободном распространении продвинутых алгоритмов поиска экстремумов? Моя реализация не всегда работает корректно.

Есть датчик, с которого снимается сигнал. Этот сигнал фильтруется (гифка прилагается), а затем осущетвляется поиск минимума для определения периодики процесса. Сигнал далек от идеального, поэтому нужен наиболее эффективный алгоритм поиска миимума. Суть вопроса сводится к следующему - нет ли в свободном распространении продвинутых алгоритмов поиска экстремумов? Моя реализация не всегда работает корректно.

Сообщение отредактировал deelan - Oct 29 2007, 10:52

Алгоритм Стронгина не подойдёт?

А где обещанная гифка? Кроме гифки укажите, минимум какой функции Вы ищите и каким алгоритмом пользуетесь.

Сори, осталась в другом посте. Немного с нажатием кнопок переусердствовал.

Я не знаю как называется мой алгоритм. Что-то типаа pattern recognition. Ищу локальный минимум, а потом проверяю по его соседям (глубина, ширина). Самопал обыкновенный, однако дает достаточно хорошие результаты, но хочется большей точности.

Изображение уменьшено 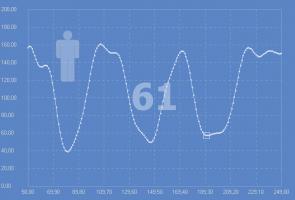(9.1 килобайт)

Для поиска экстремуму в зашумлённых данных есть ещё такая "стохастическая аппроксимация"

http://bse.sci-lib.com/article106594.html

Смесь Ньютона-Рафсона с тем фактом, что ряд
сумма a(n) расходится,
а сумма а(n)^2 сходится
Нужно много измерений

Может поможет.

ПС. Кажется метод Стронгина из той же оперы (?)

pattern recognition - это "распозначание образов". Вы ищите локальные минимумы в сигнале, потом по расстоянию между найденными минимумами вычисляете оценку его периода? Или строите некоторую периодическую функцию, в которой период - настраиваемый параметр, а потом по результатам сравнения ее с записанным сигналом вычисляете требуемое значение периода по минимуму ошибки?

Если первый случай - Ваш, то вы придумали вполне работоспособный алгоритм. Его можно только модифицировать, аналогично "методу парабол", принятому при решении оптимизационных задач. Для этого, сначала Вы ищите точку локального минимума в дисретной записи данных. Потом находите две или больше точек, стоящих по разные стороны от локального минимума по временной шкале. Значения в этих точках должны быть гарантированно больше ликального минимума, а в промежутках между локальным минимумом и этими точками не должно быть других локальных минимумов. Потом по набору найденных точек строите аппроксимирующую параболу, и находите ее минимум. Это и будет уточненная оценка локального минимума.

У меня первый сучай. Метод парабол - подойдет. Спасибо

Экстремум в реальном времени нужно искать или сигнал записывается куда-то? Нужен просто математический алгоритм или алгоритм в приложении к какому-то микроконтроллеру? Если первое, то чем нахождение первой и второй производной не устраивает?
P.S. аттач не отображается.

В общем случае ответа нет.
После предъявления статистических свойств полезного сигнала и помехи могут последовать рекомендации.

В самом примитивном случае: два фильтра, один для выделения основной частоты, второй для текущего среднего, т.е. НЧ фильтр с большой постоянной времени. Выходы сравниваются кросс-детектором.

Только для определения периода процесса поиск экстремумов сигнала не есть наилучший метод. Другие методы, скорее всего, дадут заметный выигрыш в точности. Например, поиск первого максимума автокоррреляционной функции в заданном диапазоне смещений.