Полиномы Чебышева, Почему не ортогональны? Опции

[Xenia]

Полиномы Чебышева. Почему не ортогональны?

Среди ортогональных многочленов очень часто упоминаются полиномы Чебышева (первого рода). Везде пишут примерно следующее:

Свойства многочленов Чебышева.
1. Система {Tn(x)}_n=0,1,... ортогональна на отрезке [-1,1] с весом h(x)=1/sqrt(1-x²)

Готовых функций, которые генеруют эти полиномы, всюду завались, и по сути все они делают одно и тоже. Короче говоря, сгенерила я эти полиномы от n=0 до n=5 включительно, представляя отрезок [-1,1] в виде массива дискретных элементов, достаточно длинного, чтобы эффект дескретизации сказывался слабо. Например, массив из gap=101 элемента (нечетное количество элементов выбирала для того, чтобы иметь среднюю точку). Номер элемента (i) пересчитывается в значение x из отрезка [-1,1] по формуле:
x = (double)(2*i)/(gap-1) - 1.0;
где: gap - длина массива.
Т.е. 0-й элемент массива соответствует (x=-1.0), а последний 100-й соответствует (x=+1.0). Серединка (50-й элемент) соответствует x=0.

Получилась матрица F, размером gap x 6. Если построить графики по столбцам той матрицы, то получим картинку, индентичную той, что нарисована а Википедии:
(форум не хочет эту картинку показывать)
http://ru.wikipedia.org/wiki/%D0%A4%D0%B0%...0%B0_%D0%A2.gif

Вроде бы теперь мне только жить, да радоваться . Только дернуло меня проверить эти вектора на ортогональность - вычислив продукт F*F' (размерность 6 x 6):

Код

    1.0000   -0.0000   -0.3200    0.0000   -0.0556   -0.0000
   -0.0000    0.3400   -0.0000   -0.1878    0.0000   -0.0364
   -0.3200   -0.0000    0.4722   -0.0000   -0.1686   -0.0000
    0.0000   -0.1878   -0.0000    0.4914   -0.0000   -0.1619
   -0.0556    0.0000   -0.1686   -0.0000    0.4981   -0.0000
   -0.0000   -0.0364   -0.0000   -0.1619   -0.0000    0.5016

Тут я этот продукт еще на число gap поделила, чтобы длина вектора не сказывалась.

И что вижу? Фигня какая-то... Ортогональны между собой лишь полиномы четных степеней с нечетными, а в остальных случах внедиагональные элементы слишком велики, чтобы их можно было списать на погрешность дискретизации. Впрочем, погрешность дискретизации можно еще понизить, увеличив длину вектора - тогда дискрета станет меньше. Проверила. При длине вектора gap=1001 имею:

Код

    1.0000    0.0000   -0.3320    0.0000   -0.0656   -0.0000
    0.0000    0.3340   -0.0000   -0.1988   -0.0000   -0.0466
   -0.3320   -0.0000    0.4672   -0.0000   -0.1798    0.0000
    0.0000   -0.1988   -0.0000    0.4862    0.0000   -0.1734
   -0.0656   -0.0000   -0.1798    0.0000    0.4926   -0.0000
   -0.0000   -0.0466    0.0000   -0.1734   -0.0000    0.4955

А при gap=10001:

Код

    1.0000   -0.0000   -0.3332    0.0000   -0.0666   -0.0000
   -0.0000    0.3334    0.0000   -0.1999    0.0000   -0.0475
   -0.3332    0.0000    0.4667   -0.0000   -0.1808   -0.0000
    0.0000   -0.1999   -0.0000    0.4858    0.0000   -0.1745
   -0.0666    0.0000   -0.1808    0.0000    0.4921    0.0000
   -0.0000   -0.0475   -0.0000   -0.1745    0.0000    0.4950

Куда еще дальше? Если отрезок [-1,1] представлен вектором, длиной в 10 тыс. элементов, то дискретизация становится исчезающе малой. А у меня корреляции от длины вектора практически не зависят. А корреляция между T0 и Т2 вообще ни в какие ворота не лезет -0.3332. Тем более что, если взять вместо полиномов Чебышева ряды Фурье, то даже на коротеньких массивах в 15-25 элементов ортогональность векторов очень хорошая.

Значит, это не погрешность дискретизации. Тогда что?
Где эта хваленая ортогональность, если я ее не вижу?
Не исключаю, что я здесь что-то важное недопонимаю, а потому и обращаюсь за консультацией. Что происходит? Должны ли полиномы Чебышева (первого рода) так себя вести, или мне надо продолжать искать ошибку у себя?

[_Ivana]

Глупый вопрос навскидку - вы учли

с весом h(x)=1/sqrt(1-x^2)

сразу при генерации матрицы?

[Xenia]

Глупый вопрос навскидку - вы учли
сразу при генерации матрицы?

Нет, не делила и не учитывала. Нормировкой заниматься не вижу смысла - если вектора ортогональны, то они при любой нормировке таковы. В лучшем случае, этим можно было бы достигнуть, чтобы по диагонали были точные единицы. Но тогда внедиагональное "гадости" становятся только больше, а не меньше! Да и искать ошибку было бы только труднее, если бы туда еще каких-то расчетов насовала.

Тут и без расчетов видны несуразности. Скажем, так бяка, что T0 и Т2 дают корреляцию = -0.3332.
Взглянем еще раз на картиночку: http://electronix.ru/redirect.php?http://r...0%B0_%D0%A2.gif
T0 - это красная прямая линия, уровень 1. А T2 - это желтенький, на параболу похожий. Их корреляция в уме вычисляется, т.к. умножение на 1 тривиально. В результате чего должен получиться интеграл желтого. А вы видите как широко он своим языком ниже нуля погрузился? А выше оси только по крашки чуть-чуть выпирают. Ежу ясно, что инетеграл будут не нулевой, а сильно отрицательный. Что и имеет место в расчетах.



На этой картинке (ее формум показывать не отказывается) T2 - зелененький.
Т.е. это я к тому, что сумма почленных произведений красного T0 и зеленого T2 никак не может быть равна нулю - это даже на глаз видно. А значит, они не ортогональны, как их не масштабируй по высоте.

[Alexey Lukin]

Ксения, ортогональность этих полиномов надо понимать не в обычном смысле, а после домножения на корректирующую функцию:

В дискретном же случае они ортогональны на специальной "кривой" сетке, но не на равномерной сетке.

[Xenia]

Ксения, ортогональность этих полиномов надо понимать не в обычном смысле, а после домножения на корректирующую функцию:
В дискретном же случае они ортогональны на специальной "кривой" сетке, но не на равномерной сетке.

А вы мне можете этим способом показать, что T0 и T2 ортогональны друг другу? Тем более для такого простого случая, когда T0 единичен в любой своей точке, а T2 = 2x²-1.

[_Ivana]

Те полиномы, которые нечетны, автоматически ортогональны с Т0 даже без веса (Т0 и Т1, Т0 и Т3 и т.д.) - домножение на четную функцию не изменит общий ноль интерграла - как у Вас и получилось. А другим требуется все-таки домножение на весовую функцию, как и написано выше.

[Xenia]

Те полиномы, которые нечетны, автоматически ортогональны с Т0 даже без веса (Т0 и Т1, Т0 и Т3 и т.д.) - домножение на четную функцию не изменит общий ноль интеграла - как у Вас и получилось. А другим требуется все-таки домножение на весовую функцию, как и написано выше.

А есть ли какие-нибудь "разумные" полиномы, у которых ортогональность понимается в обычном смысле? Т.е. в виде простого скалярного произведения обоих векторов, содержащих в себе расписанные по дискретам полиномы? Чтобы FF' была диагональной без всяких оговорок?
А то я такие большие планы с полиномами Чебышева связывала, и всё коту под хвост...

[_Ivana]

На Лагранжа не хотите возложить надежды и проверить его на обычную ортогональность?

[Xenia]

На Лагранжа не хотите возложить надежды и проверить его на обычную ортогональность?

Про полиномы Лагранжа я знаю только то, что их для интерполяции используют (даже когда-то их для этой цели использовала сама). Но мне сейчас не интерполировать надо, а нужен подходящий ортогональный базис из гладких функций. Поближе к обычным степенным полиномам, но только, а отличие от них, ортогональный. И чтобы его на МК можно было вычислить, а не через Гамму-фунцию или что-то еще более уродливое. Поэтому на полиномы Чебышева и запала.

Если из полиномов Лагранжа можно сотворить ортогональный базис, то меня это возможно заинтересовало бы. Что-то посоветуете конкретнее?

[_Ivana]

Насчет базиса из Лагранжа не знаю. Простите если напрасно обнадежил. Но у Лежандра вроде единичная весовая функция http://ru.wikipedia.org/wiki/%D0%9E%D1%80%...%B5%D0%BD%D1%8B

[Xenia]

Насчет базиса из Лагранжа не знаю. Простите если напрасно обнадежил. Но у Лежандра вроде единичная весовая функция http://ru.wikipedia.org/wiki/%D0%9E%D1%80%...%B5%D0%BD%D1%8B

Слава вам! Похоже на то, что полиномы Лежандра первого рода (Legendre Polynomial of the First Kind) мне бы сгодились.
Смотрим на картинку, которую я надыбала среди картинок с помощью Google:


Это отсюда - http://www.efunda.com/math/legendre/legendre.cfm

Тут зелененький T2 торчит много выше - здесь я уже поверю, что его интеграл на отрезке нулевой.

Сильно похоже на полиномы Чебышева! Только формулы там какие-то страшные, чтобы их построить.

[_Ivana]

Только формулы там какие-то страшные, чтобы их построить.

С той же ссылки Вики первые несколько многочленов

Не такие уж и страшные. А дальше вроде рекуррентная формула последующих дает надежду что и там страх нарастает не сильно.
ЗЫ картинки у меня тоже красиво не загружаются или я не умею - в общем, посмотрите сами по ссылке - очень милые полиномы.

Сообщение отредактировал _Ivana - Jul 24 2012, 21:14

[AndrewN]

Чтобы FF' была диагональной без всяких оговорок

Есть небольшая разница между функциональным (например L_2) бесконечномерным пространством и векторным конечномерным пространством. Отличие в определении метрики и нормы. То, что годится для векторного пространства (сумма произведений компонент векторов) не годится для бесконечномерного пространства, где скалярное произведение определяется как интеграл произведения комплексно сопряжённой функции на функцию (возможно, с весом).

А уж в численных методах считать интегралы методом прямоугольника (фактически - скалярное произведение конечномерных векторов) - дело плохое, из-за большой погрешности формулы. Для численного интегрирования стараются применять более точные формулы (ДФП - исключение, от плохой жизни и лёгкости факторизации матрицы, что служит основой всех быстрых алгоритмов).

Кстати, интересный факт: система обычных полиномов {1, x, x^2, ...} - оказывается, линейно независима. Следовательно к ней можно применить процесс Грама-Шмидта. Вот сюрприз-то...

[Alexey Lukin]

А вы мне можете этим способом показать, что T0 и T2 ортогональны друг другу? Тем более для такого простого случая, когда T0 единичен в любой своей точке, а T2 = 2x²-1.

Конечно: 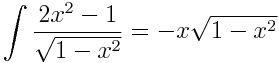Подставляем -1 и +1 и получаем 0.

Точнее, надо подставлять -1+eps и 1-eps, т.к. ортогональность берётся на интервале (-1, +1), а не на отрезке.

[AndrewN]

интервале (-1, +1), а не на отрезке

А что, уже опять поменяли определение определённого интеграла?????

[Alexey Lukin]

Ну, следовало сказать, что интеграл несобственный.

[Xenia]

Лежандр рулит!

При длине вектора 15:

Код

    1.0000   -0.0000    0.0714         0    0.0825         0
   -0.0000    0.3810         0    0.0777         0    0.0917
    0.0714         0    0.2628    0.0000    0.0870         0
         0    0.0777    0.0000    0.2187         0    0.0984
    0.0825         0    0.0870         0    0.2006    0.0000
         0    0.0917         0    0.0984    0.0000    0.1938

Шероховатости в виде внедиагональных элементов видны, но уже не такие большие, как у Чебышева, и могут быть списаны на грубость дискретизации (15 элементов это действительно мало).
Проверяем эту гипотезу, увеличивая число элементов в векторе до 101:

Код

    1.0000   -0.0000    0.0100    0.0000    0.0102   -0.0000
   -0.0000    0.3400    0.0000    0.0101    0.0000    0.0104
    0.0100    0.0000    0.2081   -0.0000    0.0103   -0.0000
    0.0000    0.0101   -0.0000    0.1517   -0.0000    0.0106
    0.0102    0.0000    0.0103   -0.0000    0.1206    0.0000
   -0.0000    0.0104   -0.0000    0.0106    0.0000    0.1009

Увеличиваем число элементов в векторе до 1001:

Код

    1.0000   -0.0000    0.0010   -0.0000    0.0010    0.0000
   -0.0000    0.3340   -0.0000    0.0010    0.0000    0.0010
    0.0010   -0.0000    0.2008    0.0000    0.0010   -0.0000
   -0.0000    0.0010    0.0000    0.1437   -0.0000    0.0010
    0.0010    0.0000    0.0010   -0.0000    0.1120    0.0000
    0.0000    0.0010   -0.0000    0.0010    0.0000    0.0918

Увеличиваем число элементов в векторе до 10001:

Код

    1.0000   -0.0000    0.0001   -0.0000    0.0001   -0.0000
   -0.0000    0.3334   -0.0000    0.0001   -0.0000    0.0001
    0.0001   -0.0000    0.2001   -0.0000    0.0001    0.0000
   -0.0000    0.0001   -0.0000    0.1429    0.0000    0.0001
    0.0001   -0.0000    0.0001    0.0000    0.1112    0.0000
   -0.0000    0.0001    0.0000    0.0001    0.0000    0.0910

Теперь совершенно очевидно, что матрица корреляции строго диагональна, а ее недостатки были вызваны исключительно грубостью дискретизации.

[_Ivana]

AndrewN а если при определенных парах полиномов с весом первообразная в +-1 будет в бесконечность улетать? Вы же написали интересные любопытные вещи, давайте не будем спорить об имхо несущественных деталях.

Xenia рад что у Вас все получилось да ещё сразу проверилось моделированием.

Сообщение отредактировал _Ivana - Jul 24 2012, 22:12

[AndrewN]

Ну, следовало сказать, что интеграл несобственный

Первообразная-то все равно без особенностей по краям. Вычислили и вычли, а несобственность (пределы eps слева-справа) держим в уме.

Увеличиваем число элементов в векторе до ...

Такой метод можно назвать "переверну Дарбу в гробу"...

[_Ivana]

ТС нужна была система ортогональных полиномов в единичным весом - она их нашла. Для чего и как применять - это уже второй вопрос. Можно ли применить более оптимальные методы для решения этой неизвестной авторской задачи - уже третий. А "Увеличиваем число элементов в векторе до ..." в этом контексте - не более чем метод проверки базиса на ортогональность, который кстати работает.

[AndrewN]

который кстати работает

Не понимаете вы чёрный юмор - то, чем занимается Xenia - вычислением в лоб сумм Дарбу, предел которых, как известно, и есть значение (и даже определение) определённого интеграла. Ну, уж было бы странно, что бы эти суммы не сходились куда надо.

[Xenia]

Такой метод можно назвать "переверну Дарбу в гробу"...

Отчего же? Интеграл изначально определялся как предел сумм при бесконечном увеличении разбиения отрезка на части. Это уж потом привыкли к разным аналитическим выражениям, черпаемых в справочниках .

А я, увеличивая длину вектора, представляющего собой разбиение отрезка [-1,+1], делала буквально то самое, что определяется, как интеграл. Правда, до бесконечности я не дошла, а остановилась на 1/10000 от ширины интервала, но с моими 4-мя знаками после запятой этот предел вполне достаточен, поскольку большей точности при таком выводе результата я все равно не увижу.

На практике же мне нужны именно суммы, а не интегралы в их аналитическом выражении. Поскольку исходные данные, которые мне придется переводить в базис Лежандра, исключительно табличные (это данные от АЦП). И для этого перевода мне придется находить скалярные произведения векторов длиной gap. Если базисные вектора достаточно хорошо ортогональны, то можно было бы не раскручивать МНК с обращением матрицы, а просто поочередно перемножать вектор данных на вектора ортогонального базиса. Поэтому в данной задаче меня больше всего волнует именно та погрешность, которая возникнет, если стану работать с базисом, как ортогонльным, в условиях, когда дискретизация представления базиса в векторах реально дает ортогонализацию с ошибкой.

[AndrewN]

А я, увеличивая длину вектора, представляющего собой разбиение отрезка [-1,+1], делала буквально то самое, что определяется, как интеграл. Правда, до бесконечности я не дошла, а остановилась на 1/10000 от ширины интервала, но с моими 4-мя знаками после запятой этот предел вполне достаточен, поскольку большей точности при таком выводе результата я все равно не увижу.

Xenia, вы прелесть (не устану это повторять), но нельзя извращать метод. А метод гласит, что раз доказано аналитически, то можно и посчитать (с ошибкой, в общем случае). Но не наоборот.

Ну в самом деле, на любом компьютере сумму гармонического ряда можно сосчитать как два пальца об асфальт, просто потому что а) суммирование элементарно приходится оборвать и б) начиная с некоторого n члены просто перестают давать вклад в бегущую сумму. "Но мы-то знаем", что ряд расходится!

исходные данные, [...] мне придется переводить в базис Лежандра

Арифметика мне понятна, вы считаете коэффициенты разложения по базису. Но что вас заставляет использовать такой неудобный базис? В этом какая-то физика замешана?

[Xenia]

Xenia, вы прелесть (не устану это повторять), но нельзя извращать метод. А метод гласит, что раз доказано аналитически, то можно и посчитать (с ошибкой, в общем случае). Но не наоборот.

Так я и не пыталась решать глобальные задачи типа сходимости неизвестных рядов. Суть была в том, что полиномы Чебышева не образуют ортогональную (в моем понимании!) систему, а в полиномы Эрмита ее образуют. За что еще раз спасибо _Ivana, что надоумил.

Проверку же на ортогональность я проводила отнюдь не ради доказательства ортогональности полиномов Эрмита (в моем смысле), а чтобы убедиться, в какой мере эта ортогональность соблюдается в "дискретном пространстве", где данные полиномы могут быть представлены единственным образом - в виде ограниченного числа точек.

В последнем случае уже не так важно, насколько ортогональны идеальные полиномы, заданные аналитически или в виде непрерывной геометрической кривой, а интерес представляет то, насколько хорошо справятся с задачей сохранения ортогональности те самые, покоцанные из-за недостатка точек, векторы.

Арифметика мне понятна, вы считаете коэффициенты разложения по базису. Но что вас заставляет использовать такой неудобный базис? В этом какая-то физика замешана?

Почему вдруг этот базис неудобный? А какой тогда удобный?

Физически задача у меня довольно тривиальная - регрессия. Т.е. я хочу "впендюрить" отрезки экспериментальной кривой в базис невысокой размерности. Так очень часто поступают, аппроксимируя экспериментальные точки прямой, параболой, реже полиномами более высоких порядков. Я тоже так делала, но недовольна сильной корреляцией между собой степенных полиномов, из-за чего обращаемая матрица становится близкой к матрице Гилберта и обращается с ошибками.

Где-то я читала, что разложение на степенные полиномы высших степеней - вообще мазохизм. И там советовали разложение на полиномы Чебышева, из коэффициентов которых можно при необходимости получить и коэффициенты степенного полинома.

А когда приступила к делу, то с ужасом обнаружила, что полиномы Чебышева не ортогональны в матричном смысле - вот и с горя затеяла эту тему. А так, по внешнему виду кривых этих полиномов они весьма схожи со кривыми степенных рядов (линией, квадратной и кубической параболой и т.д.), с той лишь разницей, что не так резво уходят вдаль на границах диапазона, а упираются концами в единицу (или минус единицу).

В вычислительном смысле хороши ряды Фурье, которые тоже образуют ортогональный базис, но практически они дают очень плохой результат из-за того, что кривая регрессии получается волнистая. А чтобы волны на ее поверхности утихомирить, нужен почти что полный набор векторов. Тогда как степенные ряды с легкостью аппроксимируют почти любые плавные изгибы экспериментальной кривой небольшим числом своих первых членов. Фурье так не может.

[AndrewN]

в базис невысокой размерности

Ага. А, кстати, можно ли посмотреть на пару-тройку файлов с измерениями - отправьте на е-мейл?

[Xenia]

А, кстати, можно ли посмотреть на пару-тройку файлов с измерениями - отправьте на е-мейл?

Посмотреть нельзя! Однако тут дело не в конкретных данных, а в самой "странно поставленной" задаче. Если хотите, то в общих чертах объясню ситуацию.

Ползет лента самописца... Только по нынешнему времени это не лента, а высокоразрядный АЦП данные снимает и на экране компьютера рисует. Ну и, как водится, сигнал шумит. Если бы это самописец был, то он бы толстую линию рисовал, т.к. перо у него ходуном бы ходило (из-за своей инерционности обычные бумажные самописцы на высокочастотный шум не реагируют, но АЦП его отлично видит).

Только не торопитесь ставить диагноз - "Так вам шум фильтровать надо? Мы это и без всяких полиномов смастырим!" Нет, не всё тут тривиально, а потому наберитесь терпения дослушать моё объяснение до конца. Так вот "задним числом" по тем сырым данным ползет окно и аппроксимирует точки/значения, в него попавшие, полиномом какой-то степени (математически это зовется регрессией). Ширина окна и степень полинома выбираются не с потолка, а исходя из определенных соображений, и в процессе продвижения окна могут автоматически изменяться в зависимости от того, насколько удачно проходит аппроксимация. Эти соображения я пока опущу. А дальше строго по статистическим критериям (там и t-критерий Стьдента и хи-квадрат пробабилити) оценивается, входит ли центральная точка в окне в доверительный интервал. Если входит, то подлежит замене на значение полинома в этой точке. Т.е. в этом случае имеет место типичное скользящее сглаживание по N-точкам полиномом n-ой степени. Но это лишь пока тишь да гладь, а шум укладывается в пределы статистической нормы. Но стоит какой-то точке или нескольким точкам не вписаться в "валютный коридор" , то их аппроксимировать уже нельзя! И рисуются такие точки, как есть, без всякого сглаживания. Такие сигналы квалифицируются, как выбросы/феномены, и их изучать придут большие ученые . И горе тому, кто сгладит выброс!

[AndrewN]

Посмотреть нельзя

Ага. 3 сигмы или две?
А если вместо странных полиномов использовать косинусное преобразование для сигнала - модели то толковой для него всё рано нету...
И почему посмотреть-то нельзя - я по временному ряду кита от стаи селёдки все равно не отличу, а любопытство заело...

[Xenia]

Ага. 3 сигмы или две?

Две сигмы ("the Inverse Student-t Probability Distribution Function (two-tail) for 5% error").

А если вместо странных полиномов использовать косинусное преобразование для сигнала - модели то толковой для него всё рано нету...

Я уже на этот счет заикалась. Косинусное, как и обычное Фурье-преобразование плохо аппроксимирует импульные скачки. Например, если вдруг "дернулось" (короткий бросок напряжения), то нет такой частоты гармоники, которая бы удовлеворительно его аппроксимировала. А в результате произойдет следующее - получится целый спектр разночастотных гармоник, имеющих синхроннизацию "выпуклости" на этом месте. С тем, значит, расчетом, чтобы на месте импульса гармоники сложились в одной полярности, а по бокам друг дружку погасили. А если я ограничу размер базиса первыми n-гармониками, то после апроксимации получу по всему полю периодическую волну с часттой младшей гармоники базиса, которую некому будет погасить. Прошу прощения за слог, но лучше объяснить на словах это являение я не могу. А вот полиномы очень прилично изображают такие "дергунчики" очень малым числом членов и не вызывают побочных эффектов в виде ряби.

И почему посмотреть-то нельзя - я по временному ряду кита от стаи селёдки все равно не отличу, а любопытство заело...

Да там и смотреть нечего. Шум типа белого с какой-то шириной амплитуды. Да еще медленный тренд в течение суток. Амплитуда шума, кстати, тоже от времени суток зависима - днем она больше, ночью меньше. Ну а если где-то ... э ... типа зелетрясение произойдет али подземный ядерный взрыв , но из того шума сразу вылезут импульсы, на остальной шум ничуточки не похожие. Т.е. сейсмические данные - очень близкий аналог моей задачи, хотя в моем случае "прослушивают" не землю, а живой организм.

Я в этой дискуссии хотела бы поиметь какой-нибудь профит, а не играть роль ответчицы, отправдывающейся перед аудиторией в том, что она делала так, как надо . Поэтому уж извините меня за стремление увести разговор от обсуждения моей работы и целесообраности применения в ней тех или иных методов, а сосредоточиться на интересующих меня полиномах. С тем расчетом, чтобы использовать ваши знания по части аналитических методов.

С этой целью я хочу попросить вас растолковать мне явление, природа которого мне не ясна. А именно речь идет о дискретных представлениях полиномиального базиса (впрочем, у гармонического базиса тоже могут быть аналогичные проблемы). А сама проблема вот в чем. В аналитическом виде (в виде формулы) дела с ортогональностью обстоит лучше некуда - считают интегралы и те показывают ортогональность базиса. Но вот я загоняю тот базис в матрицу (скажем полином каждой степени занимает в ней отдельный столбец), то ортогональности как ни бывало! А точнее говоря, как бы я аккуратно не "оцифровывала" тот полином (хоть интегралом на 1/N-ой части области), всякий раз возникает значительная ошибка, как в отношении ортогональности между собой полиномов разных степеней, так и единичной нормы в отношении каждого из полинома.

Казалось бы причина этой бяки очевидна - своей дискретизацией я нарушаю что-то такое, что в аналитическом виде было гладким, а у меня стало ступенчатым. И в пользу такого заключения вроде бы свидетельствует тот факт, что с увеличением длины векторов (числа разбиений) ортогональность повышается. Казалось бы на коротких (меньше 10-ти элементов) и речи не может быть о точной ортогональности. Однако можно легко убедиться в том, что дискретизация ортогональности не помеха. Простой пример - берем квадратную матрицу полного ранга и просим библиотечную функцию найти полный набор ее собственных векторов. И вот абсолютно в любом случае (!) ортогональность тех векторов гарантирована с вычислительной точностью. Тут и точные нули между скалярными произведениями различных векторов будут на месте и единичная норма каждого из них. Причем, не приблизительная, а совершенно точная! И при этом на малых (коротких) векторах ничуть не хуже, чем на длинных.

Выходит, что дискретное представление не мешает выбирать ортогональные базисы. Тогда почему, когда дело касается полиномов Чебышева и Лежандра, то начинает катавасия с точностью? Это плохие полиномы? Или я их плохо оцифровала? Или они вообще для этих целей непригодны из-за того, что во времена Лежандра и Чебышева компьютеров не было и численными методами они не баловались? Или все-таки в дискретном виде могут существовать "гладкие" ортогональные многочлены?

Особняком тут стоят ряды/многочлены Фурье. Почему непонятно, но вроде бы у их дискретизация никаких проблем не вызывает. Хоть из 8-ми точек будет массив, но фурьевый базис как-то ухитряется быть ортогональным. Впрочем, я не исследовала случай, когда число точек не 2ⁿ, а другое. И потому не стану на их счет что-то категорически утверждать.

Что касается вида самих полиномов Чебышева и Лежандра, но они мне вполне нравятся, но отсутствие ортогональности (в векторном смысле) делает их для моих целей неприемлемыми. Где-то слышала, что бывают дискретные преобразования в базисы Чебышева и Лежандра (например, "Discrete Chebyshev Transform" и "Discrete Legendre Transform"), но ничего подходящего пока не нашла. Хотя в отношении Лежандра наклёвывается вариант "DLOP" (аббревиатура от "Discrete Legendre Orthogonal Polynomials"), но как следует разобраться с ним не успела.

[Xenia]

В отношении дискретного представления полиномов Лежандра (DLOP = "Discrete Legendre Orthogonal Polynomials") у меня наметился прогресс. Помогли статьи, найденные мною на IEEE:
1) On the computation of discrete Legendre polynomial coefficients (1992)
2) Recursive computation of discrete Legendre polynomial coefficients (1996)

DLOPы, какой бы короткой размерности ни были, сохраняют ортогональность идеально! Правда нормы у этого базиса по построению не единичные, но это я сама виновата - не осилила вычисление весовых коэффициентов. Но нормализовать их ничего не стоит обычным способом - вычислить норму в лоб и разделить на нее. Главное, что кросс-матрица у них изначально строго диагональна, как и положено.

Тем не менее имеются определенные странности, отличающие DLOP от обычных полиномов Лежандра. И этот вопрос заслуживает отдельного опуса .

Во-первых, обычные полиномы Лежандра (как и полиномы Чебышева) определены на отрезке [-1, +1], тогда как DLOP - исключительно на положительных значениях натурального аргумента, т.е. определены дискретно на векторе/массиве ровно этой длины, для которой они строятся. Это очень удобно тем, что избавляет от необходимости постоянно пересчитывать номера элементов в X-координату на отрезок [-1, +1] и обратно.

Во-вторых, центр симметрии у обычных полиномов Лежандра (как и у полиномов Чебышева) находится точно в начале координат (в середине отрезка [-1,1]), тогда как у DLOP тоже в середине, но уже в середине вектора! Например, если вектор у нас длиной в 15 элементов, но центр симметрии будет приходиться на 7-ой элемент массива.

В-третьих, обычные полиномы Лежандра (как и полиномы Чебышева) всегда пересекаются в точке (1,1), т.е. в правом верхнем углу графика. А DLOP пересекаются всегда в 1-ом элементе вектора (в языке C у него нулевой номер). Из-за этого некоторые полиномы нечетной степени (которые раньше упирались в точку(-1,-1)) оказались перевернутыми вверх ногами.

Но в целом - красотища! Смотрим картинки.



- это обычные полиномы Лежандра, срисованные из интернета.

А полиномы DLOP, построенные по 15 точкам (array[15]), я построила сама и попытаюсь вложить в конец этого сообщения. Несмотря некоторую "корявость" представления полиномов высших степеней (4 и 5) из-за недостаточной длины вектора, ортогональность здесь превосходна!

Что же касается практических применений, то тут показательна статья
Adaptive ECG Data Compression Using Discrete Legendre Transform (2002)
в которой DLOP использованы для компрессии ЭКГ-сигнала. Как выглядит кардиограмма человека, наверняка, все знают. И по внешнему виду схожа со многими сигналами, с которыми часто приходится иметь дело: типа того, что долго не было ничего, и вдруг вигля выскочила . А применимость для компрессии подобного вида сигналов свидетельствует о том, что базис DLOP показал себя на деле даже лучше, чем требуется для целей сглаживания шумов.

Эскизы прикрепленных изображений

 

[_Ivana]

Xenia спасибо, очень интересны ваши подробные описания собственных размышлений, поисков и нахождения решений! Да ещё и с тематическики ссылками!

ЗЫ я после попытки устроить подобное (хотя нельзя считать её неудачной) подумал что на этом форуме не принято совместное коллективное исследование и решение задач. Вы возвращаете мне надежду

ЗЗЫ по делу сказать пока ничего не могу, хотя я предполагал что должны существовать красивые дискретно задаваемые ортогональные базисы с хорошими показателями нормы и ортогональности - но вы их сами уже нашли.

ЗЗЗЫ Идея Вашего метода понятна, за исключением деталей, которые на первый взгляд несущественны (типа бежим ли окном смещаясь на один отсчет входных данных или сразу кусками почти на всю длину окна - для оставления кусков перекрытия)

[Xenia]

ЗЗЫ по делу сказать пока ничего не могу, хотя я предполагал что должны существовать красивые дискретно задаваемые ортогональные базисы с хорошими показателями нормы и ортогональности - но вы их сами уже нашли.

Я бы и еще таких поискала. Наверняка, есть еще что-то подобное. Просто классические полиномы постоянно на слуху, а более редкие прозябают в безвестности. Если где-то встретите - сигнализируйте.

[_Ivana]

Во-первых, обычные полиномы Лежандра (как и полиномы Чебышева) определены на отрезке [-1, +1], тогда как DLOP - исключительно на положительных значениях натурального аргумента, т.е. определены дискретно на векторе/массиве ровно этой длины, для которой они строятся. Это очень удобно тем, что избавляет от необходимости постоянно пересчитывать номера элементов в X-координату на отрезок [-1, +1] и обратно.

А до сего момента Вы разве не так получали вектора разной длины из отрезка полиномов Чебышева и Лежандра на отрезке [-1, 1]? Странно что вы отмечаете этот момент отдельно.

Во-вторых, центр симметрии у обычных полиномов Лежандра (как и у полиномов Чебышева) находится точно в начале координат (в середине отрезка [-1,1]), тогда как у DLOP тоже в середине, но уже в середине вектора! Например, если вектор у нас длиной в 15 элементов, но центр симметрии будет приходиться на 7-ой элемент массива.

Опять же, имхо это естественное следствие дискретизации непрерывной функции. Если бы дискретизировали четным количество точек, то центр был бы между точками. Снова не понимаю, почему вы придаете значение таким имхо очевидным вещам. Или вы все ваши предыдущие вектора строили из аналитического выражения на интервале [0, 1]? Тогда у вас не могла получиться ортогональность например полинома 1 или 3 степени с полиномом 0 степени....

В-третьих, обычные полиномы Лежандра (как и полиномы Чебышева) всегда пересекаются в точке (1,1), т.е. в правом верхнем углу графика. А DLOP пересекаются всегда в 1-ом элементе вектора (в языке C у него нулевой номер). Из-за этого некоторые полиномы нечетной степени (которые раньше упирались в точку(-1,-1)) оказались перевернутыми вверх ногами.

Здесь у вас получилась аналогия с аналитическим базисом от (-х) - который тоже базис и тоже ортогонален и нормирован. Ибо четные полиномы не поменялись а нечетные остались нечетными. И все они пересекаются в точке [-1, 1].

А вот бОльшая амплитуда размаха DLOP по сравнению с обычными аналитическими полиномами Лежандра (вплоть до вылетов за границы +-1) врядли является следствием просто отсутствия нормировки (кстати, ваша картинка внизу - из нормированных DLOP или нет?). Ссылки приведенные к сожалению платные и навскидку не получилось с ними ознакомиться.

[Xenia]

А вот бОльшая амплитуда размаха DLOP по сравнению с обычными аналитическими полиномами Лежандра (вплоть до вылетов за границы +-1) врядли является следствием просто отсутствия нормировки (кстати, ваша картинка внизу - из нормированных DLOP или нет?).

Моя картинка не нормированная, хотя практически я пользуюсь номированной. Не хотела вводить нормировку в картинку, чтобы ярче были видны отличия от классических полиномов Лежандра. И, похоже, я достигла своей цели, если вы без подсказки заметили, что значения некоторых из высших полиномов ВНУТРИ интервала определения зашкаливают за единицу. Очевидно, что это не является следствием нормировки, т.к. в этом случае исчезло бы касание +1 или -1 на краях. Ведь нормируются полиномы, как кривая вдоль оси Х, а не поперек. Поэтому, если бы я путем масштабирования вызвала тот зашкал, то и на краях кривая промахнулась бы мимо единицы. А этого нет!

То, что вы заметили, является одним из важнейших достоинств DLOP над обычными полиномами Лежандра, т.к. именно этим способом первые обеспечивают себе ортогональность всегда! Тут либо ортогональность, либо удержание себя в рамках приличия. И очень отрадно, что DLOP пренебрегли приличием ради ортогональности. Ведь если подумать, то главное достоинство базиса в его отогональности и ортонормированности, а вовсе не в ограничении амплитуды единицей. Ограниченостью единичной амплитудой нас Фурье заразил. Дурной пример заразителен, и теперь каждому начинает казаться, без всяких на то оснований, что ограниченность амплитуды единицей является необходимостью. Тогда как на самом деле единицей должна быть ограничена норма, а вовсе не амплитуда.

Ссылки приведенные к сожалению платные и навскидку не получилось с ними ознакомиться.

Написали бы вы, _Ivana, заявку в "Свои", тем паче, что по всем критериям вы давно того достойны. Я на здешнем ftp такую потрясную библиотку книг по ЦОС собрала (разделы DSP и Image_processing)! И эти платные статьи тоже туда положила (вместе с другими по DLOP, которых в своих сообщениях не упоминала). ЦОС - вообще великая наука, от одного только соприкосновения с которой весь мир начинает восприниматься по-другому.

P.S. Вот здесь http://www.mathworks.com/matlabcentral/fil...expansions.html в разделе "Drawing orthogonal polynomials" только что нашла графики пронормированных полиномов Лежандра (обычные, не DLOP):



Как-то странно они их пронормировали, что сохранилось T0=1 всюду, но остальные полиномы настолько "выпучились", что перестали касаться единицы на концах. Ну, а за пределы единичного корридора вылезли кажется все, кроме нулевого.

Кстати, там я уже вижу еще новых претендентов на гладкие ортогональные полиномы. Это


полиномы Якобы (Jacobi polynomials)
и

полиномы Эрмита (Hermite polynomials)
Интересно, существуют ли их дискретные аналоги?

[_Ivana]

Изначально я вам предложил Лежандра потому что в аналитическом виде они ортогональны с единичной весовой функцией, именно то что вас не устроило в Чебышеве. Дискретные аналоги Чебышева вы читали, Лежандра тоже. У Эрмита и Якоби тоже должны существовать дискретные аналоги, но в аналитическом виде они ортогональны с отличной от единицы весовой функцией, то есть в этом смысле "не лучше" Чебышева. Если вы в вашем методе сможете использовать такие "условно" ортогональные дискретные полиномы - тогда сможете попробовать и Чебышева и Эрмита с Якоби.

Тогда как на самом деле единицей должна быть ограничена норма, а вовсе не амплитуда.

Именно так. И в этом смысле не стоит цепляться за единицу на краях, ибо она не нужна. Другое дело, если нужны нормированные полиномы высоких степеней и частая дискретизация, а полиномы в краях интервала идут "вразнос" и значения получаются слишком большими - но думаю до этого дойти надо постараться

Про отличие DLOP от Лежандра у меня есть некие ассоциации. Во первых, я подозреваю что чем больше точек в векторе, тем эти отличия меньше (по крайней мере, в окрестности нуля). Во вторых, это очень похоже (метафизически ) на интерполяцию через обрезанный синк и синк с окном - обрезанный синк дает плохое качество интерполяции, а те же полиномы Лагранжа при увеличении своего порядка представляют собой синк умноженный на окно Гаусса (что я случайно обнаружил). Так если мы возьмем мало точек, посчитаем по ним обрезанный синк - будет плохо, а догадаться умножить эти значения на некоторое окно, которое "подправит" этот дискретный массив в нужную сторону - надо ещё суметь, к тому же Гаусс - далеко не единственное окно в природе. Мне кажется что примерно по аналогичному принципу рассчитываются DLOP из обычного Лежандра. Поэтому вполне возможно (хотя и не факт), что можно придумать ещё другие дискретные ортогональные базисы с единичной весовой функцией. Хотя мне кажется ваша задача легко решится и с помощью DLOP.

ЗЫ я тоже думал насчет заявки в "Свои", но не решался. Спасибо за приглашение и доверие

[Xenia]

Тут есть еще одно перспективное направление для копания. Суть лежит в некоем родстве полиномов с ... рядами Фурье. В самом деле, если и далее растягивать тот "гамак" , сплетенный из полиномов, увеличивая одновременно число точек в векторе и количество степеней полиномов, то они все больше становятся похожими на гармоники. Разве что с деформацией на "краевой эффект". Вот такая у них получается огибающая:



Отсюда могут вытекать методы, основанные на проведении на первой стадии преобразования Фурье (прямого или обратного), а затем какой-то замысловатой комбинации над полученными коэффициентами Фурье. Или наоборот - сначала проводятся замысловатые масштабирования и/или перестановки элементов, а преобразование Фурье уже потом.

Вот какой любопытный алгоритм я надыбала в интернете, хотя далеко не уверена, что он рабочий. Привожу его код (на MatLab'е) полностью, поскольку исполнямых в нем всего 3 строки.

Код

function uh = fct(u)
% Fast Chebyshev Transform
%
%    uh : Discrete Chebyshev Transform Coefficients.
%    u  : Function values evaluted at Chebyshev Gauss Lobatto nodes
%         with nodes ordered increasingly x_i=[-1,...,1}
%         for i=1,2...,N
%
% By Allan P. Engsig-Karup, apek@imm.dtu.dk.

N  = length(u);
u  = ifft([u([N:-1:1 2:N-1])]); % reverse ordering due to Matlab's fft
uh = ([u(1); 2*u(2:(N-1)); u(N)]);
return

http://www.mathworks.com/matlabcentral/fil...t/content/fct.m
Это якобы быстрое преобразование Чебышева. Одно только название чего стоит! Суть алгоритма состоит в том, что к преобразуемому массиву слева дописывают его зеркальное отражение (первый элемент остается в центре, не удваиваясь), а справа последний элемент удаляют (его отражение сохранится в отражении). А потом то, что получилось, скармливают обратному преобразованию Фурье (функция ifft). Результат увеличивают в масштабе вдвое, за исключением крайних точек, и дело в шляпе. Неужели так просто?

Несмотря на очевидность стадий алгоритма, его суть мне совершенно непонятна, хотя очень здОрово, если это работает.

[Alexey Lukin]

Суть в том, что на специальной сетке точек, для которой полиномы Чебышева ортогональны, умножение на полином Чебышева сводится к умножению на косинус. Соответственно, преобразование Чебышева сводится к ДКП 2 рода, что и продемонстрировано в вашем коде, где ДКП (неэффективно) вычисляется через ДПФ.

[Xenia]

Суть в том, что на специальной сетке точек, для которой полиномы Чебышева ортогональны, умножение на полином Чебышева сводится к умножению на косинус. Соответственно, преобразование Чебышева сводится к ДКП 2 рода, что и продемонстрировано в вашем коде, где ДКП (неэффективно) вычисляется через ДПФ.

Отрадно, что вы упомянули в этой связи DCT-2. Я к нему тоже приглядывалась, но отвергла из-за отсутствия в их базисе "линейного" полинома - прямой наклонной линии:



Тогда как в базисах Чебышева и Лежандра такой полином есть. Причина моего неприятия чисто практическая - при измерениях на большой чувствительности наблюдается значительный линейный тренд. И вина на это ложится не столько на измерительный комплекс (хотя и он сам тоже такой тренд имеет), сколько на саму экспериментальную установку. Т.е. избавиться от тренда на физическом уровне не удается, но его можно легко удалить при обработке данных. Для этого даже не нужно переходить в другие базисы - достаточно просто вычесть нижний "треугольник".

Базис Лежандра хорош тем, что линейный наклон полностью ложится на "линейный" полином T1 (наклонную линию). Достаточно обнулить вклад этого полинома, чтобы тренд исчез, не повредив ничего остального. А вот в базисах, где наклонной линии нет, всем базисам полного набора приходится совместно трудиться над тем, чтобы воспроизвести наклонный тренд. И это очень плохо для меня! Хотелось бы, чтобы в отсутствии полезного сигнала (линейный тренд полезным сигналом не считается) высшие полиномы нагрузки не несли. Лежандр или Чебышев в этом отношении хороши - младшие полиномы T0 (горизонталь) и T1 (наклонная линия) берут на себя аппроксимацию тренда. А при анализе их вклады можно было просто не учитывать.

А вот базис Фурье уже плох тем, что нет у него наклонной линии. Из-за этого простенький пример, представляющий собой наклонную линию, превращается в базисе Фурье в монстра, где все базисы возбуждены в стремлении изобразить наклонную линию, которая этому базису чужда.

К моему глубокому сожалению, базис DCT-2, хотя и лучше Фурье, но полностью этого недостатка не лишен. Причина в том, что его собственный T1, хотя и похож на наклонную линию, но на самом деле представляет собой половинку периода косинуса. Поэтому его загибание на концах приходится компенсировать возбуждением всех остальных участников базиса.

Может быть, вам известны какие-либо фурье-подобные базисы, в которых младшие два элемента базиса были бы горизонтальной (T0) и наклонной линией (T1)? А то, судя по названию DCT-2, возможны и другие DCT. Вдруг среди них есть требуемое? Сама же я нашла лишь описание базисов от DCT-1 до DCT-4, которые требуемым качеством не обладают.

[Xenia]

P.S. Отчего бы не сотворить такой базис на отрезке [-1,+1]: T0 - прямая линия (уровень +1), T1 - наклонная линия от точки (-1,-1) через начало координат до точки (+1,+1), а остальные - косинусы с целым числом периодов (чтобы были четными функциями). Т.е. то, что получится, если удалить из базиса DCT элементы, изображенные на рисунке справа (т.к. они нечетные), добавив наклонную линию. На мой взгляд, такой базис должен быть ортогональным, поскольку наклонная линия, пересекающая начало координат, ортогональна любой четной функции, а косинус - именно такая функция.

Известен ли в мире такой базис? И если да, то как он называется? Или же я ошиблась относительно его ортогональности?

P.P.S. Кажется, я чушь сморозила - базисом с одними четными функциями (одного нечетного T1 среди них недостаточно) нечетные функции вряд ли аппроксимируешь.