широкополосные жаропрочные линзы(коллиматоры), фторопласт? еще что-то есть пригодное? Опции

[Hale]

Какой посоветуете неплохой доступный материал для широкополосной фокусировки в пределах нескольких метров на 10-20 ГГц при установке на рупор?
Условиях эксплуатации я бы это описал как 6 круга ада, раскаленные контролируемые объекты и наличие водяных паров с примесью окислителя.
до сих пор рупоры затыкали термостеклом, но без коллиматора плохо работает.

[Hale]

Одну вы используете для фокусировки. Вторая-на преобразование амплитудного распределения или оптимизации

Это не так. Так используют сферические линзы в оптике. На свч это решение неэффективно.
Обе поверхности выполняют и функцию коллимирования, и выравнивания амплитуд.

я сейчас проверил, удивительную вещь заметил. мениск не получается никак по решению Зелкина.

Изначально я обнаружил, что требуется три условия для определения задачи. Но ошибочно взял за третье к-т отражения. Это привлекательный вариант, но он не даст точного решения задачи. Я забыл, что углы хода луча от обеих поверхностей в линзе должны совпадать. Это и есть третье условие (кроме условия фазы и равномерного распределения)
Но решить эту задачу просто не получается.

А решение у Зелкина - похоже что очень ловкая аппроксимация точного решения. Я подозреваю, что он стянул его из какой-то оптической книжки, у какого-нибкдь Люнеберга, или Аббе. И не указал источника, поэтому так незаметно воткнуто, как будто пустячок. Вообще, практическое отсутствие в книжке ссылок (всего 30 ссылок ссылок на 300 страниц) настораживает.

[l1l1l1]

...
А решение у Зелкина - похоже что очень ловкая аппроксимация точного решения. Я подозреваю, что он стянул его из какой-то оптической книжки, у какого-нибкдь Люнеберга, или Аббе. И не указал источника, поэтому так незаметно воткнуто, как будто пустячок. Вообще, практическое отсутствие в книжке ссылок (всего 30 ссылок ссылок на 300 страниц) настораживает.

уважаемый Hale! а давайте не будем возвращаться к моральному облику Зелкина, ныне покойного!
работает решение Зелкина, или не работает?

[Hale]

уважаемый Hale! а давайте не будем возвращаться к моральному облику Зелкина, ныне покойного!
работает решение Зелкина, или не работает?

О моральном облике ничего не говорю. Говорю только то что по какой-то причине (в СССР таких было полно, начиная от борьбы с космополитизмом) он использовал решение из неизвестного источника без каких-либо пояснений.

Как точное решение оно не годится. Как аппроксимация - годится. Но хорошо работает в узких пределах фокуса порядка диаметра линзы.

Далее, я почти неделю бился над решением этой задачи. Моих знаний математики не хватает чтобы проинтегрировать дифференциал поверхности с несколькими зависимыми переменными. Или что то же, продифференцировать условие равенства фаз, где все параметры взаимно зависимы.

Поэтому я стал решать задачу численными приращениями... И 4 раза обломал зубы. Дело в том, что как ты не суммируй эти дифференциалы по поверхности, решение расходится. Если с самого начала не появляется пила, то линза неестественно загибается ближе к оси симметрии.


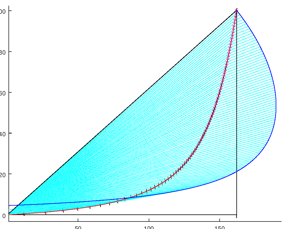
Тогда я поступил совсем тупо в лоб. Задал дифференциалы на основе приращения, гарантировав этим непрерывность дифференциала поверхности.
И все условия, 1) равенство фаз 2А) отклонение луча найденное из дифференциала поверхности 1, 2Б)отклонение луча найденное из дифференциала поверхности 2; где 2А=2Б закатал в fsolve из Octave (нелинейный метод Пауэла).
Метод страшно неустойчив, не обладает границами и взвешиванием.
Но я уже знаю что затравка на краю линзы где-то около половинного угла отклонения луча.
Ну и решилось! Точная поверхность для точечного оптического источника.

Для сравнения, вот график отношения угла луча в линзе (к оптической оси) и угла луча от источника. Здесь Ноль слева - ось, направление направо - к краю линзы.


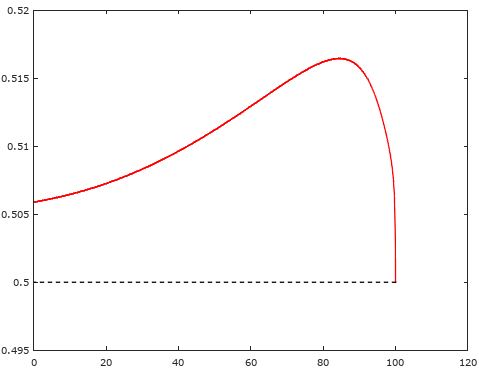
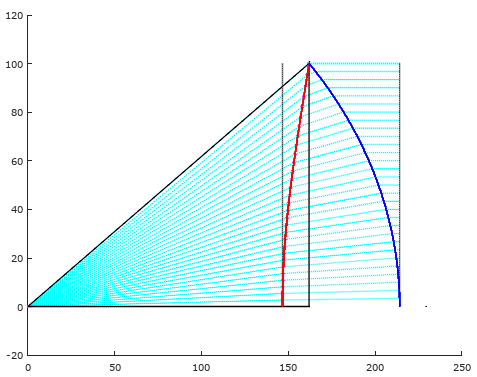
Как вы видите, половинное отклонение - несколько грубая аппроксимация, приводящая к накоплению ошибки в середине линзы. То что Зелкин и показал на заключительных графиках. В реальности этот загиб к 1/2 задан руками. Точное решение должно начинаться где-то от 0.53 (т.е. угол/1.89).

Чтобы вы понимали степень неточности "решения" из книжки, истинный график отношения угла луча в линзе к углу от источника:


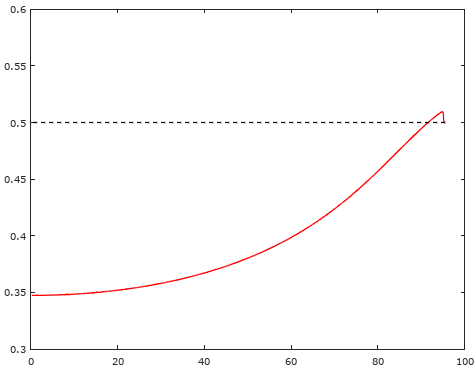
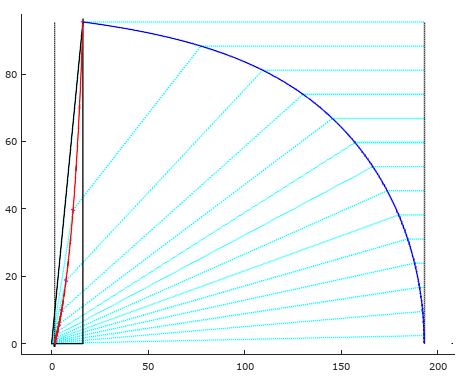
Половиной тут даже не пахнет. В реальности линза будет напоминать волчок. Что кстати хорошо скажется на прохождении с уменьшением отражения.

Кстати, узнаете в ней полусферическую диэлектрическую антенну для планарных возбудителей? Это ассимптотическое решение. Только теперь вы знаете, что небольшой конус, упирающийся в возбуждающий элемент идет на пользу.
Еще одно кстати. Мениск получится при очень больших значениях проницаемости, 4 и выше при типичных размерах рупора.

Теперь мне интересно, как корректно построить решение для трехмерной линзы с неравными шириной и высотой. А также будет ли она работать с вырезанными зонами френеля. Вырезать-то придется под углом, вдоль хода лучей. Функция несколько исказится.

P.S.
вы всегда должны помнить, что процессоры Intel - говеные вычислители синусов. Отсюда и проблемы с оптимизацией и сходимостью. Где только возможно, надо сводить тригонометрию к теореме Пифагора.