Несколько вопросов по обработке NMEA Опции

[Alt.F4]

Добрый день.
$GPRMC,181057.000,A,5545.2389,N,03745.6063,E,0.47,74.50,190311,,,A*51
1. Подскажите пожалуйста, какое максимальное кол-во символов в следующих параметрах NMEA полученных от GPS-применика:
а) Широта
в) Долгота
с) Скорость
2. Как можно рассчитать расстояние между 2-мя полученными координатами широты/долготы?
Спасибо.

Сообщение отредактировал Alt.F4 - Jul 17 2011, 04:32

[MKdemiurg]

1) зачем вам символы - вырезайте между запятыми. Я в своём парсере так и делал.
2) Когда для диплома "навигатор" делал , сделал так:

Поиск расстояния между 2 координатами.

// Константы, используемые для вычисления смещения и расстояния
const double D2R=0.017453; // Константа для преобразования градусов в радианы
const double R2D=57.295781; // Константа для преобразования радиан в градусы
const double a=6378137.0; // Основные полуоси
const double b=6356752.314245; // Неосновные полуоси
const double e2=0.006739496742337; // Квадрат эксцентричности эллипсоида
const double f=0.003352810664747; // Выравнивание эллипсоида

Код

double DIST(double StartLat, double StartLong, double EndLat, double EndLong)
{
double fPhimean,            // Средняя широта
fdLambda,                  // Разница между двумя значениями долготы
fdPhi,                     // Разница между двумя значениями широты
fAlpha,                    // Смещение
fRho,                      // Меридианский радиус кривизны
fNu,                       // Поперечный радиус кривизны
fR,                        // Радиус сферы Земли
fz,                        // Угловое расстояние от центра сфероида
fTemp,                     // Временная переменная, использующаяся в вычислениях
Distance;                  // Вычисленное расстояния в метрах

unsigned char S[20];

// Вычисляем разницу между двумя долготами и широтами и получаем среднюю широту
fdLambda=(StartLong - EndLong)*D2R;
fdPhi=(StartLat - EndLat)*D2R;
fPhimean=((StartLat + EndLat)/2.0)*D2R;

// Вычисляем меридианные и поперечные радиусы кривизны средней широты
fTemp=1-e2*(pow(sin(fPhimean),2));
fRho=(a*(1-e2))/pow(fTemp, 1.5);
fNu=a/(sqrt(1-e2*(sin(fPhimean)*sin(fPhimean))));
// Вычисляем угловое расстояние                                        
fz=sqrt(pow(sin(fdPhi/2.0),2)+cos(EndLat*D2R)*cos(StartLat*D2R)*pow(sin(fdLambda/2.0),2));
fz=2*asin(fz);
// Вычисляем смещение
fAlpha=cos(EndLat*D2R)*sin(fdLambda)*1/sin(fz);
fAlpha=asin(fAlpha);
// Вычисляем радиус Земли
fR=(fRho*fNu)/((fRho*pow(sin(fAlpha),2))+(fNu*pow(cos(fAlpha),2)));
// Получаем расстояние
Distance=(fz*fR);
return Distance;                                                    
};

Вот так вычислял азимут (незнаю насколько правильно), весь смысл в формировании местной системы координат . осями которой являются хорды паралельные параллелям и меридианам:

Код

double Azimut(double StartLat, double StartLong, double EndLat, double EndLong)
{
double AZ;
double OX,OY;
unsigned char S[20];
OX=DIST(StartLat, StartLong, StartLat, EndLong);
OY=DIST(StartLat, StartLong, EndLat, StartLong);
if (StartLat<=EndLat)
        {
        if (StartLong<=EndLong)
                        {
                        AZ=atan(OX/OY)*R2D;
                        }
                        else
                        {
                        AZ=360-atan(OX/OY)*R2D;
                        };
        }
        else
        {
        if (StartLong<=EndLong)
                        {
                        AZ=180-atan(OX/OY)*R2D;
                        }
                        else
                        {
                        AZ=180+atan(OX/OY)*R2D;
                        };
        };  

return AZ;                
};

ЗЫ С гуглоземлёй сходилось, точность не замерял - не было смысла - диплом , не коммерческий прожект. Кое где код можно оптимизировать ( И я молодой был и компилятор тупил)

Сообщение отредактировал MKdemiurg - Jul 17 2011, 09:03

[Alt.F4]

1. Подскажите пожалуйста, какое максимальное кол-во символов в следующих параметрах NMEA полученных от GPS-применика:
а) Широта
в) Долгота
с) Скорость

1) зачем вам символы

Чтобы знать, сколько байт выделить в СОЗУ под это дело.

2) Когда для диплома "навигатор" делал , сделал так:

Попробую на след.выходных...

Сообщение отредактировал Alt.F4 - Jul 17 2011, 07:11

[sobr]

Добрый день.
$GPRMC,181057.000,A,5545.2389,N,03745.6063,E,0.47,74.50,190311,,,A*51
1. Подскажите пожалуйста, какое максимальное кол-во символов в следующих параметрах NMEA полученных от GPS-применика:
а) Широта
в) Долгота
с) Скорость

Я понимаю так, что количество символов не изменно, оно определено стандартом, символы либо есть, либо нет.

[MKdemiurg]

Чтобы знать, сколько байт выделить в СОЗУ под это дело.

Ну так выделите больше. Я брал массив вырезал от запятой до запятой. Отделял градусы вотдельный массив из 3х(или 4 для долготы) байт. В конце вставлял /0 (определитель конца строки - ноль). Использовал массивы градусов и минут как входные переменные функции преобразования в число. На выходе получал double - вполне удовлетворительная точность (теоретически). Складывал градусы и доли градусов от преобразования минут.

Я понимаю так, что количество символов не изменно, оно определено стандартом, символы либо есть, либо нет.

Изменно - в разных приёмниках бывает разное кол-во символов после десятичной точки.

Сообщение отредактировал MKdemiurg - Jul 17 2011, 09:57

[sobr]

Изменно - в разных приёмниках бывает разное кол-во символов после десятичной точки.

Ваша правда, дробная част переменной длины.

[Alt.F4]

Ну так выделите больше.

Насколько больше?
Интересует конкретные цифры:
- широта (вроде как 9 символов с точкой максимум)
- долгота (аналогично, только 10. Хотя первый ноль можно исключить, мне до туда не доехать =)
- скорость (5 с точкой максимум)
Спасибо.

Сообщение отредактировал Alt.F4 - Jul 17 2011, 14:50

[MKdemiurg]

Насколько больше?
Интересует конкретные цифры:
- широта (вроде как 9 символов с точкой максимум)
- долгота (аналогично, только 10)
- скорость (5 с точкой максимум)
Спасибо.

Я брал так как вы и написали 9 и 10 (для долготы). Для уверенности ( так сказать чтобы парсер не "завис") можно вырезать ровно по 4 цифры после точки-разделителя.
А вообще можно посчитать для конкретной точности, остальное отбрасывать.

[Alt.F4]

А что со скоростью, сколько максимум символов после запятой, два?

[MKdemiurg]

Вообще два символа после запятой. Я один обрабатывал. Т.к. опять же точности хватало. А вообще это зависит от приёмника и кол-ва выборок для расчёта. Он всёравно даёт усреднёную скорость. Если хотите точности - ставте акселерометр электронный. Стоит то какихто 100-120 грн.

ЗЫ Вообще 0.01 от узла - это 0.005м\с - 5мм\с - я сомневаюсь, что GPS приёмники на такое способны.

Сообщение отредактировал MKdemiurg - Jul 17 2011, 17:08

[Alt.F4]

Вообще 0.01 от узла - это 0.005м\с - 5мм\с

0,01 узлов = (0,01/1,852)км/ч = 0.0054 км/ч = 1,5 мм/с

Сообщение отредактировал Alt.F4 - Jul 17 2011, 19:19

[MKdemiurg]

Брр,чот не так , подожь.

1,852км/ч/3600=0,514(4) м/с
0,514*0.01=0.00514м/с=5.14мм/с - НЕ?

(0,01/1,852)км/ч = 0.0054 км/ч

(0,01/1,852)км/ч = 0,01852 км/ч.

Кароче неважно, без реперных точек и поправок такая точность невозможна.

Сообщение отредактировал MKdemiurg - Jul 17 2011, 19:39

[Alt.F4]

А ё, это надо умножать на 1,852...

[V_G]

Если не зацикливаться на NMEA, то в любом приемнике есть бинарный протокол, дающий геоцентрические координаты в метрах, по которым легко посчитать дистанцию без трехэтажных формул преобразования из географических координат. И скорость часто бывает в км/ч.

А в NMEA разные приемники могут давать разное число знаков после точки. Что в широте/долготе, что в скорости

[MKdemiurg]

Если не зацикливаться на NMEA, то в любом приемнике есть бинарный протокол, дающий геоцентрические координаты в метрах, по которым легко посчитать дистанцию без трехэтажных формул преобразования из географических координат. И скорость часто бывает в км/ч.

Это вы про SIRF ? - далеко не во всех. А вот NMEA - во всех.

[V_G]

Ну, я предпочитаю выбирать те девайсы, которые удовлетворяют определенным требованиям. Во всех них стоят достаточно мощные процессоры, рассчитывающие координаты в геоцентрической системе, и лишь потом пересчитывающие в географические (для NMEA, например). А потом мы своей прогой на слабом процессоре пытаемся делать обратное преобразование - зачем?
Хотя платим за скорость и точность вычислений потерей универсальности, согласен.

[MKdemiurg]

Ну, я предпочитаю выбирать те девайсы, которые удовлетворяют определенным требованиям. Во всех них стоят достаточно мощные процессоры, рассчитывающие координаты в геоцентрической системе, и лишь потом пересчитывающие в географические (для NMEA, например). А потом мы своей прогой на слабом процессоре пытаемся делать обратное преобразование - зачем?
Хотя платим за скорость и точность вычислений потерей универсальности, согласен.

Ну так , насколько я знаю, во всех приёмниках сначала вычисляются геоцентрические координаты. Просто не во всех есть бинарный протокол.
А вернуть из NMEA в геоцентрические координаты не требует особых ресурсов. Мне Atmega16 хватало чтобы всю математику реализовать ,включая поправки. Но вообще вы правы - sirf удобнее для вычислений.

[Frolov Kirill]

Выше какие-то попросту бредовые утверждения. Да, в декартовой системе координат посчитать расстояние между двумя точками можно и без арктангенса и т.п. Но какой в этом смысл, если это будет наикратчайшее расстояние по-прямой, при том, что интересует скорей путь на поверхности сферы (эллипсоида) земли?

Если расстояния маленькие (единицы-десятки километров) и погрешности допустимы большие, то можно посчитать "широтный радиус", домножив на косинус (всё в целых числах, 16 бит) получить координаты в декартовой системе и посчитать расстояние для плоскости...

Иначе считать как написано здесь, например, (http://gis-lab.info/qa/great-circles.html) и не морочить мозг. Хотя арктангенс в целых числах можно тоже написать и всё остальное тоже -- овчинка выделки не стоит, проще #include <math.h> И не надо притягивать SIRF за уши, он абсолютно ничем не поможет, в полярных координатах даже проще.

Сообщение отредактировал Frolov Kirill - Jul 18 2011, 11:44

[V_G]

Ну, вообще-то дистанция между двумя точками на расстоянии сотен-тысяч километров мало кого интересует. Интересует пробег, т.е. сумма дистанций по достаточно частым засечкам (километр - два максимум, иначе о пробеге говорить смысла нет). А в этом случае расчет в декартовых координатах гораздо точнее.
MKdemiurg
Про atmeg'у 16 конечно, правильное утверждение, но только в том случае, если процессору нечем заняться, кроме как координаты пересчитывать. Для моих задач это всего одна из многих функций, и я предпочту освободить процессорное время для их реализации вместо повторного обратного пересчета.

P.S. специально для Frolov Kirill.
Земля не имеет форму шара. При преобразованиях координат используются модели Земли в виде различных эллипсоидов: WGS-84, Красовского (предпочтительны для нашей страны) и пр. Так что действительно точные расчеты по географическим координатам несколько сложнее, чем в приведенной Вами ссылке.

P.P.S. Особенно в этой ссылке умиляет радиус Земли, приведенный с точностью до метра, когда разность большой и малой полуосей эллипсоида WGS-84 составляет более 21 километра.

Сообщение отредактировал V_G - Jul 18 2011, 13:57

[MKdemiurg]

Выше какие-то попросту бредовые утверждения. Да, в декартовой системе координат посчитать расстояние между двумя точками можно и без арктангенса и т.п. Но какой в этом смысл, если это будет наикратчайшее расстояние по-прямой, при том, что интересует скорей путь на поверхности сферы (эллипсоида) земли?

Если расстояния маленькие (единицы-десятки километров) и погрешности допустимы большие, то можно посчитать "широтный радиус", домножив на косинус (всё в целых числах, 16 бит) получить координаты в декартовой системе и посчитать расстояние для плоскости...

Иначе считать как написано здесь, например, (http://gis-lab.info/qa/great-circles.html) и не морочить мозг. Хотя арктангенс в целых числах можно тоже написать и всё остальное тоже -- овчинка выделки не стоит, проще #include <math.h> И не надо притягивать SIRF за уши, он абсолютно ничем не поможет, в полярных координатах даже проще.

Ну так а кто вам сказал, что расстояния в сотни км высчитываються как хорда? Всё зависит от точности. Можно разбить путь по апроксимирующему эллипсоиду на сотни или тысячи точек с меньшим расстояние между собой ( на цифровых картах используються точки "перелома").

[Alt.F4]

Дак по какой конкретной формуле будет точнее всего рассчитать небольшое расстояние (от 10м до 1км), зная широту и долготу?
По следующей чтоле, взятой отсюда, как посоветовал Frolov Kirill?


Сообщение отредактировал Alt.F4 - Jul 18 2011, 14:39

[MKdemiurg]

Дак по какой конкретной формуле будет точнее всего рассчитать небольшое расстояние (от 10м до 1км), зная широту и долготу?
По следующей чтоле, взятой отсюда, как посоветовал Frolov Kirill?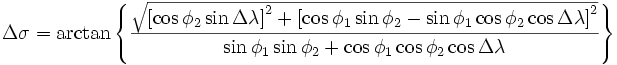

Только это для поверхности апроксимирующего эллипсоида, а у вас есть ещё и высота на уровнем моря. + к тому отклонения идеального элипсоида от реальной земной поверхности. Гораздо точнее разбить весь путь на маленькие отрезки ( с цифровыми картами это даже проще) и сложить их длины. Если совсем маленькие - то на кривизну можно забить и считать как на 1 странице я выложил код "усреднённого" расстояния. Гораздо проще. Можно также строить сектора в декартвой системе и находить длины дуг сектора (при этом можно ещё и высоту ввести в расчёты) и складывать потом.

[Alt.F4]

Если совсем маленькие - то на кривизну можно забить и считать как на 1 странице я выложил код "усреднённого" расстояния.

По большому счету, я думаю до 1км на кривизну можно точно забивать.
А откуда Ваши формулы (с 1-ой страницы) взяты?
Спасибо.

[MKdemiurg]

По большому счету, я думаю до 1км на кривизну можно точно забивать.
А откуда Ваши формулы (с 1-ой страницы) взяты?
Спасибо.

Оттуда же, http://gis-lab.info/qa/great-circles.html. Ну точнее , это общеизвестные формулы. Я брал ещё из гофман-гелленгофф "Глобальная система определения местоположения". А код реализованный есть ещё под pascal в сети. Переделал для себя под С.

2. Формула гаверсинусов

Используется, чтобы избежать проблем с небольшими расстояниями.

Дополню, точнее уточню.
По этой формуле вы получаете угловую разницу. А потом зная приближённый радиус для данной широты - ищете дугу.

Сообщение отредактировал MKdemiurg - Jul 18 2011, 16:54

[Alt.F4]

MKdemiurg, а, дак Вы как раз и использовали формулу, которую я "скопипастил" в пост_21.
Просто сразу не вчитывался в Ваш листинг...
Значит будем юзать ее.
Спасибо.

Сообщение отредактировал Alt.F4 - Jul 18 2011, 17:06