Добрый день.
$GPRMC,181057.000,A,5545.2389,N,03745.6063,E,0.47,74.50,190311,,,A*51
1. Подскажите пожалуйста, какое максимальное кол-во символов в следующих параметрах NMEA полученных от GPS-применика:
а) Широта
в) Долгота
с) Скорость
2. Как можно рассчитать расстояние между 2-мя полученными координатами широты/долготы?
Спасибо.
Полная версия этой страницы: Несколько вопросов по обработке NMEA
Форум разработчиков электроники ELECTRONIX.ru > Интерфейсы > Форумы по интерфейсам > Сотовая связь и ее приложения
1) зачем вам символы - вырезайте между запятыми. Я в своём парсере так и делал.
2) Когда для диплома "навигатор" делал , сделал так:
Поиск расстояния между 2 координатами.
// Константы, используемые для вычисления смещения и расстояния
const double D2R=0.017453; // Константа для преобразования градусов в радианы
const double R2D=57.295781; // Константа для преобразования радиан в градусы
const double a=6378137.0; // Основные полуоси
const double b=6356752.314245; // Неосновные полуоси
const double e2=0.006739496742337; // Квадрат эксцентричности эллипсоида
const double f=0.003352810664747; // Выравнивание эллипсоида
Вот так вычислял азимут (незнаю насколько правильно), весь смысл в формировании местной системы координат . осями которой являются хорды паралельные параллелям и меридианам:
ЗЫ С гуглоземлёй сходилось, точность не замерял - не было смысла - диплом , не коммерческий прожект. Кое где код можно оптимизировать ( И я молодой был и компилятор тупил)
2) Когда для диплома "навигатор" делал , сделал так:
Поиск расстояния между 2 координатами.
// Константы, используемые для вычисления смещения и расстояния
const double D2R=0.017453; // Константа для преобразования градусов в радианы
const double R2D=57.295781; // Константа для преобразования радиан в градусы
const double a=6378137.0; // Основные полуоси
const double b=6356752.314245; // Неосновные полуоси
const double e2=0.006739496742337; // Квадрат эксцентричности эллипсоида
const double f=0.003352810664747; // Выравнивание эллипсоида
Код
double DIST(double StartLat, double StartLong, double EndLat, double EndLong)
{
double fPhimean, // Средняя широта
fdLambda, // Разница между двумя значениями долготы
fdPhi, // Разница между двумя значениями широты
fAlpha, // Смещение
fRho, // Меридианский радиус кривизны
fNu, // Поперечный радиус кривизны
fR, // Радиус сферы Земли
fz, // Угловое расстояние от центра сфероида
fTemp, // Временная переменная, использующаяся в вычислениях
Distance; // Вычисленное расстояния в метрах
unsigned char S[20];
// Вычисляем разницу между двумя долготами и широтами и получаем среднюю широту
fdLambda=(StartLong - EndLong)*D2R;
fdPhi=(StartLat - EndLat)*D2R;
fPhimean=((StartLat + EndLat)/2.0)*D2R;
// Вычисляем меридианные и поперечные радиусы кривизны средней широты
fTemp=1-e2*(pow(sin(fPhimean),2));
fRho=(a*(1-e2))/pow(fTemp, 1.5);
fNu=a/(sqrt(1-e2*(sin(fPhimean)*sin(fPhimean))));
// Вычисляем угловое расстояние
fz=sqrt(pow(sin(fdPhi/2.0),2)+cos(EndLat*D2R)*cos(StartLat*D2R)*pow(sin(fdLambda/2.0),2));
fz=2*asin(fz);
// Вычисляем смещение
fAlpha=cos(EndLat*D2R)*sin(fdLambda)*1/sin(fz);
fAlpha=asin(fAlpha);
// Вычисляем радиус Земли
fR=(fRho*fNu)/((fRho*pow(sin(fAlpha),2))+(fNu*pow(cos(fAlpha),2)));
// Получаем расстояние
Distance=(fz*fR);
return Distance;
};
{
double fPhimean, // Средняя широта
fdLambda, // Разница между двумя значениями долготы
fdPhi, // Разница между двумя значениями широты
fAlpha, // Смещение
fRho, // Меридианский радиус кривизны
fNu, // Поперечный радиус кривизны
fR, // Радиус сферы Земли
fz, // Угловое расстояние от центра сфероида
fTemp, // Временная переменная, использующаяся в вычислениях
Distance; // Вычисленное расстояния в метрах
unsigned char S[20];
// Вычисляем разницу между двумя долготами и широтами и получаем среднюю широту
fdLambda=(StartLong - EndLong)*D2R;
fdPhi=(StartLat - EndLat)*D2R;
fPhimean=((StartLat + EndLat)/2.0)*D2R;
// Вычисляем меридианные и поперечные радиусы кривизны средней широты
fTemp=1-e2*(pow(sin(fPhimean),2));
fRho=(a*(1-e2))/pow(fTemp, 1.5);
fNu=a/(sqrt(1-e2*(sin(fPhimean)*sin(fPhimean))));
// Вычисляем угловое расстояние
fz=sqrt(pow(sin(fdPhi/2.0),2)+cos(EndLat*D2R)*cos(StartLat*D2R)*pow(sin(fdLambda/2.0),2));
fz=2*asin(fz);
// Вычисляем смещение
fAlpha=cos(EndLat*D2R)*sin(fdLambda)*1/sin(fz);
fAlpha=asin(fAlpha);
// Вычисляем радиус Земли
fR=(fRho*fNu)/((fRho*pow(sin(fAlpha),2))+(fNu*pow(cos(fAlpha),2)));
// Получаем расстояние
Distance=(fz*fR);
return Distance;
};
Вот так вычислял азимут (незнаю насколько правильно), весь смысл в формировании местной системы координат . осями которой являются хорды паралельные параллелям и меридианам:
Код
double Azimut(double StartLat, double StartLong, double EndLat, double EndLong)
{
double AZ;
double OX,OY;
unsigned char S[20];
OX=DIST(StartLat, StartLong, StartLat, EndLong);
OY=DIST(StartLat, StartLong, EndLat, StartLong);
if (StartLat<=EndLat)
{
if (StartLong<=EndLong)
{
AZ=atan(OX/OY)*R2D;
}
else
{
AZ=360-atan(OX/OY)*R2D;
};
}
else
{
if (StartLong<=EndLong)
{
AZ=180-atan(OX/OY)*R2D;
}
else
{
AZ=180+atan(OX/OY)*R2D;
};
};
return AZ;
};
{
double AZ;
double OX,OY;
unsigned char S[20];
OX=DIST(StartLat, StartLong, StartLat, EndLong);
OY=DIST(StartLat, StartLong, EndLat, StartLong);
if (StartLat<=EndLat)
{
if (StartLong<=EndLong)
{
AZ=atan(OX/OY)*R2D;
}
else
{
AZ=360-atan(OX/OY)*R2D;
};
}
else
{
if (StartLong<=EndLong)
{
AZ=180-atan(OX/OY)*R2D;
}
else
{
AZ=180+atan(OX/OY)*R2D;
};
};
return AZ;
};
ЗЫ С гуглоземлёй сходилось, точность не замерял - не было смысла - диплом , не коммерческий прожект. Кое где код можно оптимизировать ( И я молодой был и компилятор тупил)
Цитата
Цитата
1. Подскажите пожалуйста, какое максимальное кол-во символов в следующих параметрах NMEA полученных от GPS-применика:
а) Широта
в) Долгота
с) Скорость
1) зачем вам символыа) Широта
в) Долгота
с) Скорость
Цитата
2) Когда для диплома "навигатор" делал , сделал так:
Попробую на след.выходных...
Добрый день.
$GPRMC,181057.000,A,5545.2389,N,03745.6063,E,0.47,74.50,190311,,,A*51
1. Подскажите пожалуйста, какое максимальное кол-во символов в следующих параметрах NMEA полученных от GPS-применика:
а) Широта
в) Долгота
с) Скорость
Я понимаю так, что количество символов не изменно, оно определено стандартом, символы либо есть, либо нет.$GPRMC,181057.000,A,5545.2389,N,03745.6063,E,0.47,74.50,190311,,,A*51
1. Подскажите пожалуйста, какое максимальное кол-во символов в следующих параметрах NMEA полученных от GPS-применика:
а) Широта
в) Долгота
с) Скорость
Чтобы знать, сколько байт выделить в СОЗУ под это дело.
Ну так выделите больше. Я брал массив вырезал от запятой до запятой. Отделял градусы вотдельный массив из 3х(или 4 для долготы) байт. В конце вставлял /0 (определитель конца строки - ноль). Использовал массивы градусов и минут как входные переменные функции преобразования в число. На выходе получал double - вполне удовлетворительная точность (теоретически). Складывал градусы и доли градусов от преобразования минут.
Я понимаю так, что количество символов не изменно, оно определено стандартом, символы либо есть, либо нет.
Изменно - в разных приёмниках бывает разное кол-во символов после десятичной точки.
Цитата
Ну так выделите больше.
Насколько больше?Интересует конкретные цифры:
- широта (вроде как 9 символов с точкой максимум)
- долгота (аналогично, только 10. Хотя первый ноль можно исключить, мне до туда не доехать =)
- скорость (5 с точкой максимум)
Спасибо.
Насколько больше?
Интересует конкретные цифры:
- широта (вроде как 9 символов с точкой максимум)
- долгота (аналогично, только 10)
- скорость (5 с точкой максимум)
Спасибо.
Интересует конкретные цифры:
- широта (вроде как 9 символов с точкой максимум)
- долгота (аналогично, только 10)
- скорость (5 с точкой максимум)
Спасибо.
Я брал так как вы и написали 9 и 10 (для долготы). Для уверенности ( так сказать чтобы парсер не "завис") можно вырезать ровно по 4 цифры после точки-разделителя.
А вообще можно посчитать для конкретной точности, остальное отбрасывать.
А что со скоростью, сколько максимум символов после запятой, два?
Вообще два символа после запятой. Я один обрабатывал. Т.к. опять же точности хватало. А вообще это зависит от приёмника и кол-ва выборок для расчёта. Он всёравно даёт усреднёную скорость. Если хотите точности - ставте акселерометр электронный. Стоит то какихто 100-120 грн.
ЗЫ Вообще 0.01 от узла - это 0.005м\с - 5мм\с - я сомневаюсь, что GPS приёмники на такое способны.
ЗЫ Вообще 0.01 от узла - это 0.005м\с - 5мм\с - я сомневаюсь, что GPS приёмники на такое способны.
Цитата
Вообще 0.01 от узла - это 0.005м\с - 5мм\с
0,01 узлов = (0,01/1,852)км/ч = 0.0054 км/ч = 1,5 мм/с
Брр,чот не так , подожь.
1,852км/ч/3600=0,514(4) м/с
0,514*0.01=0.00514м/с=5.14мм/с - НЕ?
(0,01/1,852)км/ч = 0,01852 км/ч.
Кароче неважно, без реперных точек и поправок такая точность невозможна.
1,852км/ч/3600=0,514(4) м/с
0,514*0.01=0.00514м/с=5.14мм/с - НЕ?
Цитата
(0,01/1,852)км/ч = 0.0054 км/ч
(0,01/1,852)км/ч = 0,01852 км/ч.
Кароче неважно, без реперных точек и поправок такая точность невозможна.
А ё, это надо умножать на 1,852...
Если не зацикливаться на NMEA, то в любом приемнике есть бинарный протокол, дающий геоцентрические координаты в метрах, по которым легко посчитать дистанцию без трехэтажных формул преобразования из географических координат. И скорость часто бывает в км/ч.
А в NMEA разные приемники могут давать разное число знаков после точки. Что в широте/долготе, что в скорости
А в NMEA разные приемники могут давать разное число знаков после точки. Что в широте/долготе, что в скорости
Если не зацикливаться на NMEA, то в любом приемнике есть бинарный протокол, дающий геоцентрические координаты в метрах, по которым легко посчитать дистанцию без трехэтажных формул преобразования из географических координат. И скорость часто бывает в км/ч.
Это вы про SIRF ? - далеко не во всех. А вот NMEA - во всех.
Ну, я предпочитаю выбирать те девайсы, которые удовлетворяют определенным требованиям. Во всех них стоят достаточно мощные процессоры, рассчитывающие координаты в геоцентрической системе, и лишь потом пересчитывающие в географические (для NMEA, например). А потом мы своей прогой на слабом процессоре пытаемся делать обратное преобразование - зачем?
Хотя платим за скорость и точность вычислений потерей универсальности, согласен.
Хотя платим за скорость и точность вычислений потерей универсальности, согласен.
Ну, я предпочитаю выбирать те девайсы, которые удовлетворяют определенным требованиям. Во всех них стоят достаточно мощные процессоры, рассчитывающие координаты в геоцентрической системе, и лишь потом пересчитывающие в географические (для NMEA, например). А потом мы своей прогой на слабом процессоре пытаемся делать обратное преобразование - зачем?
Хотя платим за скорость и точность вычислений потерей универсальности, согласен.
Хотя платим за скорость и точность вычислений потерей универсальности, согласен.
Ну так , насколько я знаю, во всех приёмниках сначала вычисляются геоцентрические координаты. Просто не во всех есть бинарный протокол.
А вернуть из NMEA в геоцентрические координаты не требует особых ресурсов. Мне Atmega16 хватало чтобы всю математику реализовать ,включая поправки. Но вообще вы правы - sirf удобнее для вычислений.
Выше какие-то попросту бредовые утверждения. Да, в декартовой системе координат посчитать расстояние между двумя точками можно и без арктангенса и т.п. Но какой в этом смысл, если это будет наикратчайшее расстояние по-прямой, при том, что интересует скорей путь на поверхности сферы (эллипсоида) земли?
Если расстояния маленькие (единицы-десятки километров) и погрешности допустимы большие, то можно посчитать "широтный радиус", домножив на косинус (всё в целых числах, 16 бит) получить координаты в декартовой системе и посчитать расстояние для плоскости...
Иначе считать как написано здесь, например, (http://gis-lab.info/qa/great-circles.html) и не морочить мозг. Хотя арктангенс в целых числах можно тоже написать и всё остальное тоже -- овчинка выделки не стоит, проще #include <math.h> И не надо притягивать SIRF за уши, он абсолютно ничем не поможет, в полярных координатах даже проще.
Если расстояния маленькие (единицы-десятки километров) и погрешности допустимы большие, то можно посчитать "широтный радиус", домножив на косинус (всё в целых числах, 16 бит) получить координаты в декартовой системе и посчитать расстояние для плоскости...
Иначе считать как написано здесь, например, (http://gis-lab.info/qa/great-circles.html) и не морочить мозг. Хотя арктангенс в целых числах можно тоже написать и всё остальное тоже -- овчинка выделки не стоит, проще #include <math.h> И не надо притягивать SIRF за уши, он абсолютно ничем не поможет, в полярных координатах даже проще.
Ну, вообще-то дистанция между двумя точками на расстоянии сотен-тысяч километров мало кого интересует. Интересует пробег, т.е. сумма дистанций по достаточно частым засечкам (километр - два максимум, иначе о пробеге говорить смысла нет). А в этом случае расчет в декартовых координатах гораздо точнее.
MKdemiurg
Про atmeg'у 16 конечно, правильное утверждение, но только в том случае, если процессору нечем заняться, кроме как координаты пересчитывать. Для моих задач это всего одна из многих функций, и я предпочту освободить процессорное время для их реализации вместо повторного обратного пересчета.
P.S. специально для Frolov Kirill.
Земля не имеет форму шара. При преобразованиях координат используются модели Земли в виде различных эллипсоидов: WGS-84, Красовского (предпочтительны для нашей страны) и пр. Так что действительно точные расчеты по географическим координатам несколько сложнее, чем в приведенной Вами ссылке.
P.P.S. Особенно в этой ссылке умиляет радиус Земли, приведенный с точностью до метра, когда разность большой и малой полуосей эллипсоида WGS-84 составляет более 21 километра.
MKdemiurg
Про atmeg'у 16 конечно, правильное утверждение, но только в том случае, если процессору нечем заняться, кроме как координаты пересчитывать. Для моих задач это всего одна из многих функций, и я предпочту освободить процессорное время для их реализации вместо повторного обратного пересчета.
P.S. специально для Frolov Kirill.
Земля не имеет форму шара. При преобразованиях координат используются модели Земли в виде различных эллипсоидов: WGS-84, Красовского (предпочтительны для нашей страны) и пр. Так что действительно точные расчеты по географическим координатам несколько сложнее, чем в приведенной Вами ссылке.
P.P.S. Особенно в этой ссылке умиляет радиус Земли, приведенный с точностью до метра, когда разность большой и малой полуосей эллипсоида WGS-84 составляет более 21 километра.
Выше какие-то попросту бредовые утверждения. Да, в декартовой системе координат посчитать расстояние между двумя точками можно и без арктангенса и т.п. Но какой в этом смысл, если это будет наикратчайшее расстояние по-прямой, при том, что интересует скорей путь на поверхности сферы (эллипсоида) земли?
Если расстояния маленькие (единицы-десятки километров) и погрешности допустимы большие, то можно посчитать "широтный радиус", домножив на косинус (всё в целых числах, 16 бит) получить координаты в декартовой системе и посчитать расстояние для плоскости...
Иначе считать как написано здесь, например, (http://gis-lab.info/qa/great-circles.html) и не морочить мозг. Хотя арктангенс в целых числах можно тоже написать и всё остальное тоже -- овчинка выделки не стоит, проще #include <math.h> И не надо притягивать SIRF за уши, он абсолютно ничем не поможет, в полярных координатах даже проще.
Если расстояния маленькие (единицы-десятки километров) и погрешности допустимы большие, то можно посчитать "широтный радиус", домножив на косинус (всё в целых числах, 16 бит) получить координаты в декартовой системе и посчитать расстояние для плоскости...
Иначе считать как написано здесь, например, (http://gis-lab.info/qa/great-circles.html) и не морочить мозг. Хотя арктангенс в целых числах можно тоже написать и всё остальное тоже -- овчинка выделки не стоит, проще #include <math.h> И не надо притягивать SIRF за уши, он абсолютно ничем не поможет, в полярных координатах даже проще.
Ну так а кто вам сказал, что расстояния в сотни км высчитываються как хорда? Всё зависит от точности. Можно разбить путь по апроксимирующему эллипсоиду на сотни или тысячи точек с меньшим расстояние между собой ( на цифровых картах используються точки "перелома").
Дак по какой конкретной формуле будет точнее всего рассчитать небольшое расстояние (от 10м до 1км), зная широту и долготу?
По следующей чтоле, взятой отсюда, как посоветовал Frolov Kirill?
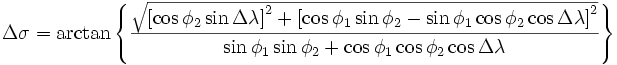
По следующей чтоле, взятой отсюда, как посоветовал Frolov Kirill?
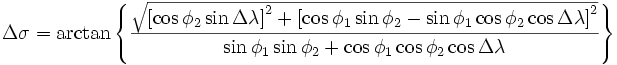
Дак по какой конкретной формуле будет точнее всего рассчитать небольшое расстояние (от 10м до 1км), зная широту и долготу?
По следующей чтоле, взятой отсюда, как посоветовал Frolov Kirill?
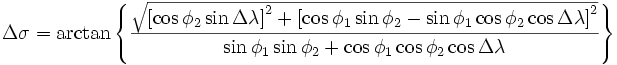
По следующей чтоле, взятой отсюда, как посоветовал Frolov Kirill?
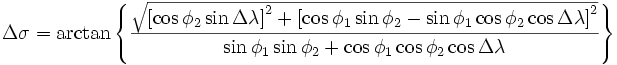
Только это для поверхности апроксимирующего эллипсоида, а у вас есть ещё и высота на уровнем моря. + к тому отклонения идеального элипсоида от реальной земной поверхности. Гораздо точнее разбить весь путь на маленькие отрезки ( с цифровыми картами это даже проще) и сложить их длины. Если совсем маленькие - то на кривизну можно забить и считать как на 1 странице я выложил код "усреднённого" расстояния. Гораздо проще. Можно также строить сектора в декартвой системе и находить длины дуг сектора (при этом можно ещё и высоту ввести в расчёты) и складывать потом.
Цитата
Если совсем маленькие - то на кривизну можно забить и считать как на 1 странице я выложил код "усреднённого" расстояния.
По большому счету, я думаю до 1км на кривизну можно точно забивать.А откуда Ваши формулы (с 1-ой страницы) взяты?
Спасибо.
По большому счету, я думаю до 1км на кривизну можно точно забивать.
А откуда Ваши формулы (с 1-ой страницы) взяты?
Спасибо.
А откуда Ваши формулы (с 1-ой страницы) взяты?
Спасибо.
Оттуда же, http://gis-lab.info/qa/great-circles.html. Ну точнее , это общеизвестные формулы. Я брал ещё из гофман-гелленгофф "Глобальная система определения местоположения". А код реализованный есть ещё под pascal в сети. Переделал для себя под С.
Цитата
2. Формула гаверсинусов
Используется, чтобы избежать проблем с небольшими расстояниями.
Используется, чтобы избежать проблем с небольшими расстояниями.
Дополню, точнее уточню.
По этой формуле вы получаете угловую разницу. А потом зная приближённый радиус для данной широты - ищете дугу.
MKdemiurg, а, дак Вы как раз и использовали формулу, которую я "скопипастил" в пост_21.
Просто сразу не вчитывался в Ваш листинг...
Значит будем юзать ее.
Спасибо.
Просто сразу не вчитывался в Ваш листинг...
Значит будем юзать ее.
Спасибо.
Для просмотра полной версии этой страницы, пожалуйста, пройдите по ссылке.
