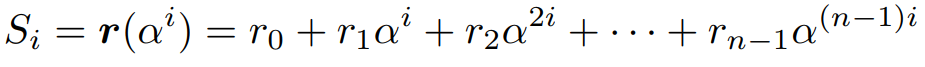Все зависит от того, как именно у вас рассчитан генераторный полином. Если вы брали корни полинома как a^[0:check] то и синдромы нужно считать для корней со степенями [0:check], если a^[1:check+1] то соответственно будет сдвиг.
ИМХО нужно вычислять все, могу ошибаться. Думаю что гуру поправят %)
ИМХО нужно вычислять все, могу ошибаться. Думаю что гуру поправят %)
Если в рекомендации указан следующий порождающий полином
Нажмите для просмотра прикрепленного файла Правильно ли я понимаю что надо считать с alfa^0?
Если у вас 2^128 разных синдромов, то ровно столько различных
ошибок может исправлять код. Там могут быть и ошибки веса много больше Dмин/2.
Исправить все можно, например, полным перебором кодовых слов (если много свободного времени )
)
Чем больше Dмин, тем дальше код от плотной упаковки и тем больше тяжелых ошибок (больше Dмин/2)
он в принципе может исправлять.
Вообще, не обязательно исправлять совсем все ошибки для хорошего декодера.
Есть , например, такой результат: достаточно исправлять все ошибки,
которые может исправить код, до веса Dвг,тогда вероятность ошибки декодирования не более чем вдвое
превосходит вероятность ошибки при декодировании полным перебором.
Здесь Dвг означает мин. расст. для данного кода, которое получается
из границы Варшамова-Гильберта для данных кодовых параметров.
Другое дело, что ваш конкретный алгоритм исправляет только часть этих ошибок.
Наример, он не исправляет ошибки веса больще Dмин/2.
Но если вы не будете в алгоритме испрользовать часть синдрома,
то часть исправимых алгоритмом ошибок еще больше уменьшится,
т.е. вы не сможете исправлять даже некоторые ошибки веса меньше Dмин/2.
ошибок может исправлять код. Там могут быть и ошибки веса много больше Dмин/2.
Исправить все можно, например, полным перебором кодовых слов (если много свободного времени
Чем больше Dмин, тем дальше код от плотной упаковки и тем больше тяжелых ошибок (больше Dмин/2)
он в принципе может исправлять.
Вообще, не обязательно исправлять совсем все ошибки для хорошего декодера.
Есть , например, такой результат: достаточно исправлять все ошибки,
которые может исправить код, до веса Dвг,тогда вероятность ошибки декодирования не более чем вдвое
превосходит вероятность ошибки при декодировании полным перебором.
Здесь Dвг означает мин. расст. для данного кода, которое получается
из границы Варшамова-Гильберта для данных кодовых параметров.
Другое дело, что ваш конкретный алгоритм исправляет только часть этих ошибок.
Наример, он не исправляет ошибки веса больще Dмин/2.
Но если вы не будете в алгоритме испрользовать часть синдрома,
то часть исправимых алгоритмом ошибок еще больше уменьшится,
т.е. вы не сможете исправлять даже некоторые ошибки веса меньше Dмин/2.
Можете объяснить, что значит плотная упаковка кода и почему чем больше Dmin, тем больше ошибок можно исправить за пределами исправляющей способности кода?