Добрый день!
Стоит задача осуществить быстрое преобразовние Фурье для 500 отсчетов. Аппаратно DSP поддерживает быстрое преобразование по модулю 2. Вопрос, как довести кол-во точек до 512? Достаточно ли заполнить недостающие значения нулями? Сильно ли исказится результат преобразования после такого допущения? Если можно ссылкой на математическое обоснование поделитесь плз. Или все таки придется до 512 точек дополнять интерполировав существующие значения? Кто чем может помогите плз.
Полная версия этой страницы: Быстрое преобразование Фурье не для степени 2
Форум разработчиков электроники ELECTRONIX.ru > Цифровая обработка сигналов - ЦОС (DSP) > Алгоритмы ЦОС (DSP)
Нулей добавить - нормально. Фактически это означает результат преобразования интерполировать.
Разрешение, конечно, при этом не увеличивается, но результат получается адекватный.
Разрешение, конечно, при этом не увеличивается, но результат получается адекватный.
Стоит задача осуществить быстрое преобразование Фурье для 500 отсчетов.
А мне нули не нравятся, спектр совсем другой. Существует множество алгоритмов для 500 отсчетов, например Винограда(раза в полтора медленнее чем FFT на 512 точек), или FFTW (http://www.fftw.org)авторы называют его самым быстрым для любого числа точек и текст программы приведен.
Чем больше добавляется нулей, тем точнее получается спектр сигнала. Конечно, это тот же самый спектр, но на более плотной сетке частот.
Чем больше добавляется нулей, тем точнее получается спектр сигнала. Конечно, это тот же самый спектр, но на более плотной сетке частот.
Ну конечно же нет. Более того, это вообще не спектр, а дпф. А степень близости дпф к спектру определяется не количеством дополнительных нулей, а числом отсчетов исследуемого сигнала. Обсуждалось это 100500 раз в том числе и на страницах данного форума.
thermit, вы что-то не в кассу... Результат ДПФ — это и есть спектр.
GetSmart, какая палка?
fontp правильно написал.
Sergey Makarov, всё зависит от задачи. В абсолютном большинстве задач выгоднее дополнить сигнал нулями, чем считать FFT "неправильного" размера.
GetSmart, какая палка?
fontp правильно написал.
Sergey Makarov, всё зависит от задачи. В абсолютном большинстве задач выгоднее дополнить сигнал нулями, чем считать FFT "неправильного" размера.
Ничего не искажается! Наоборот, становится видно больше правильных деталей. А спектры некоторых сигналов (например, ядер фильтров) без дополнения их нулями перед ДПФ вообще некорректно рассматривать.
Спасибо большое за ответы! Кое что уже началось проясняться Не могли бы еще ответить на один небольшой вопрос. Есть массив из 500 точек, грубо говоря это отсчеты для 50тигерцового сигнала с отсчетом 40 мкс за один период. А мне надо допустим разложить сигнал с основной частотой 30Гц, тогда массив получается 833 точки на один период. Для сигнала с еще меньшей частотой, массив будет еще больше. Отсюда вопрос, надо ли знать для преобразования Фурье частоту раскладываемого сигнала? или в результате разложения частота основной гармоники и так станет известной? Вроде как судя по формулам частота раскладываемого сигнала нигде не фигурирует, а делается предположение что массив данных отсчетов значений функций это есть значения за одни период, и дальше этот сигнал будет повторяться. ТО есть я могу для 30герцового сигнала взять теже 500 отсчетов? или минимум должен взять кол-во отсчетов снятое за период сигнала? Извините за дилетантские вопросы, с обработкой цифровых сигналов пока столкнулся впервые.
Не могли бы еще ответить на один небольшой вопрос. Есть массив из 500 точек, грубо говоря это отсчеты для 50тигерцового сигнала с отсчетом 40 мкс за один период. А мне надо допустим разложить сигнал с основной частотой 30Гц, тогда массив получается 833 точки на один период. Для сигнала с еще меньшей частотой, массив будет еще больше. Отсюда вопрос, надо ли знать для преобразования Фурье частоту раскладываемого сигнала? или в результате разложения частота основной гармоники и так станет известной? Вроде как судя по формулам частота раскладываемого сигнала нигде не фигурирует, а делается предположение что массив данных отсчетов значений функций это есть значения за одни период, и дальше этот сигнал будет повторяться. ТО есть я могу для 30герцового сигнала взять теже 500 отсчетов? или минимум должен взять кол-во отсчетов снятое за период сигнала? Извините за дилетантские вопросы, с обработкой цифровых сигналов пока столкнулся впервые.
спасибо за приведенную ссылку но вопрос заключался немного в другом, есть аппаратная реализация в ДСП по алгоритму двойки, и мне надо довести 500 отсчетов до 512 каким то образом, чтоб не тратиь вычеслительные ресурсы контроллера, используя аппаратный модуль.
но вопрос заключался немного в другом, есть аппаратная реализация в ДСП по алгоритму двойки, и мне надо довести 500 отсчетов до 512 каким то образом, чтоб не тратиь вычеслительные ресурсы контроллера, используя аппаратный модуль.
согласен с вами. А например я могу весь диапазон измеряемых сигналов дискретировать 512 отсчетами? буть то 10Гц сигнал, либо 60Гц. Сильно это будет влять на точность результата?
спасибо за приведенную ссылку
всё зависит от задачи. В абсолютном большинстве задач выгоднее дополнить сигнал нулями, чем считать FFT "неправильного" размера.
согласен с вами. А например я могу весь диапазон измеряемых сигналов дискретировать 512 отсчетами? буть то 10Гц сигнал, либо 60Гц. Сильно это будет влять на точность результата?
Сильно это будет влять на точность результата?
Это зависит от того, что Вы называете точностью. И какую точность считаете достаточной.
Если Вы уточните Ваши требования, то ответ будет более правильный. Может БПФ совсем не обладает требуемой точностью.
А Alexey Lukin привел пример конечного сигнала (ядро фильтра) тут и дополнять нечего слева и справа от ядра только нули.
Это зависит от того, что Вы называете точностью. И какую точность считаете достаточной.
Если Вы уточните Ваши требования, то ответ будет более правильный. Может БПФ совсем не обладает требуемой точностью.
А Alexey Lukin привел пример конечного сигнала (ядро фильтра) тут и дополнять нечего слева и справа от ядра только нули.
Если Вы уточните Ваши требования, то ответ будет более правильный. Может БПФ совсем не обладает требуемой точностью.
А Alexey Lukin привел пример конечного сигнала (ядро фильтра) тут и дополнять нечего слева и справа от ядра только нули.
первоначально хотел бы добавить что анализируемый сигнал является результатом оцифровки синусоидальных токов и напряжений во время частотного регулирования электроприводом, а преобразование фурье необходимо для анализа основных гармоник (например пяти) составляющих этот сигнал с исключением оставшихся, для последующей развертки и анализа сигнала
Цитата
Alexey Lukin:
Результат ДПФ — это и есть спектр.
Результат ДПФ — это и есть спектр.
Как скажете...
В книге Гольденберга 1985г на стр.220, если не выполняется условие 2^N дополняют массив нулями при спектральном анализе, но вот нет математического обоснования данного требования. Как я понимаю автор темы просит дать математич.обоснование разрешения дополнения массива до нужного размера какими то величинами.
анализируемый сигнал является результатом оцифровки синусоидальных токов и напряжений во время частотного регулирования электроприводом,
Гармоники весьма малы. И дополнение нулями и ресемплинг по Фарроу с обычным FFT пожалуй неприемлемы по точности.
Можно попробовать 6 нулей слева + сигнал + 6 нулей справа и применить окно с низкими значениями по краям Натолла например.
Хотя для определения гармоник лучше использовать окно флаттоп.
В книге Гольденберга 1985г на стр.220, если не выполняется условие 2^N дополняют массив нулями при спектральном анализе, но вот нет математического обоснования данного требования. Как я понимаю автор темы просит дать математич.обоснование разрешения дополнения массива до нужного размера какими то величинами.
Если отвлечься от того тонкого вопроса насколько ДПФ вообще соответствует физическому спектру сигнала.
То в книге Марпла "обосновыется" для значительного, кратного добавления нулей. В этом случае очевидно.
Смысл в том, что если изначально было N точек, то было и N ортогональных функций базиса, и по этому базису можно разложить всё что угодно, в том числе и те добавленые новые гармоники, соответствующие длине сигнала 2*N
Там в чистом виде синки взвешивают
В случае некратного дополнения на пальцах трудно сказать, но принцип примерно тот же - один базис выражается через другой. Если это расписать, то и получится, не то что доказательство, а представление сигнала через соответствующие "спектры"
первоначально хотел бы добавить что анализируемый сигнал является результатом оцифровки синусоидальных токов и напряжений во время частотного регулирования электроприводом, а преобразование фурье необходимо для анализа основных гармоник (например пяти) составляющих этот сигнал с исключением оставшихся, для последующей развертки и анализа сигнала
Для сингулярных спектров типа синусов (ширина спектра меньше бина) ДПФ в чистом виде (без спектральных окон) не является вообще адекватным инструментом анализа. Результат будет полностью зависить от того куда палка легла по отношению к бину ДПФ (не даст соврать гурукилер)
Нужно использовать спектральные окна (и, возможно, добавление большого числа нулей и интерполяцию спектра, если нужно получить измерительную точность оценки частот и амплитуд)
Размазывая спектр шире бина окном, мы получаем стабильные результаты, пусть даже теряя в разрешении.
Если просто посмотреть - достаточно добавить нулей и взвесить окном.
Если нужно промерять синусоиды с предельной точностью - то по ссылке
https://ccrma.stanford.edu/STANM/stanm/node3.html
исчерпывающее исследование
как все сложно. Многое надо обновить в памяти, информацию к размышлению я уже получил от вас. Прежде чем я займусь реализацией алгоритма на ДСП, прошу ответьте на вопрос. Все таки для анализа сигнала посредством ДПФ необходимо брать отсчеты за период этого сигнала и доводить их степени двойки?или можно использовать фиксированное окно из 512 отсчетов полученный в результате оцифровки?
дать математич.обоснование разрешения дополнения массива до нужного размера какими то величинами.
Ну все просто: ошибка = спектр обнуленного куска сигнала. Если обнуляется при переходе через нуль, то мало, а если на максимуме, то больше.
Самый простой совет: синхронизировать начало семплирования с переходом через нуль и вставлять Ваши нули перед сигналом. Ошибки останутся, но гармоники прыгать перестанут.
Все таки для анализа сигнала посредством ДПФ необходимо брать отсчеты за период этого сигнала и доводить их степени двойки?или можно использовать фиксированное окно из 512 отсчетов полученный в результате оцифровки?
Да хоть нечетное число. Если у Вас есть алгоритм БПФ на это число отсчетов, то получите результат быстрее, если нет, то по точкам можете посчитать. Если вставите нули - получите ошибку в зависимости от того какой участок сигнала так представили.
Тема измерения гармоник силовой сети обсуждалась. Резюме: использовать окно флаттоп и достаточное число отсчетов, чтобы широкие лепестки флаттоп не пересекались. Максимумы спектра и есть нужные Вам амплитуды гармоник.
Ничего не искажается! Наоборот, становится видно больше правильных деталей. А спектры некоторых сигналов (например, ядер фильтров) без дополнения их нулями перед ДПФ вообще некорректно рассматривать.
Оставим в покое ядра фильтров.
Но по поводу "становится видно больше правильных деталей" очень любопытно.
ДПФ/БПФ всего лишь свёртка с синусом aka интеграл. Ну а если мы зануляем часть функции, то с чего бы это результат интеграла функции не изменится? В ДПФ/БПФ в конце идёт нормировка результата и она расчитана на 2^n, допустим 512 точек. Синус исходника был на интервале 500 точек. Значит ошибка нормировки 500/512 = 0,97656. Иногда это неважно, иногда очень важно. А уж если кто-то пожелает в разы увеличивать блок нулями в своих корыстных целях, то вообще мама не горюй.
Но это вообще-то пока ещё мелкий недостаток, который легко перенормируется. Гораздо серьёзней, когда блоки дополняются нулями и из них выцепляются низшие гармоники. Тут уже идут значительные фазовые искажения в дополнение к амплитудным. На 1-2-3 гармониках блока, хотя в зависимости от желаемой точности и на 10-20 (грубо говоря).
Оконные функции само собой сильно улучшают ситуацию тем, что они львиную долю информации берут из центра блока, а нули дополняются по краю/краям.
Для сингулярных спектров типа синусов (ширина спектра меньше бина) ДПФ в чистом виде (без спектральных окон) не является вообще адекватным инструментом анализа. Результат будет полностью зависить от того куда палка легла по отношению к бину ДПФ (не даст соврать гурукилер)
Гурукиллер Вас всегда поправит
А вообще, что за дискриминация спектров? Все спектры имеют право встречаться в жизненных ситуациях.
Вот пример глюков "Что такое эффект размазывания"
http://psi-logic.narod.ru/fft/fft9.htm
ИМХО, непрерывный спектр существует только у частотно-модулированных сигналов или недооцифрованных. Но у недооцифрованных это просто недостаток информации уже после оцифровки. Если взять исходный аналоговый сигнал и оцифровать его точнее, то спектр "очистится" и в пределе станет прерывным. Суть в том, что многие сигналы в идеале такие, но идеально их восстановить оцифровкой очень трудно и порой не нужно. А нужно понимать с какой точностью получился результат и от чего он зависит. То бишь с какой точностью получается результат при пользовании каким-то инструментом, например БПФ, да ещё и с добавлением нулей.
Чутьё мне подсказывает, что частотно-модулированные сигналы, возможно, могут тоже выродиться в прерывные, но уже по обратной причине. Из-за переоцифровки, то бишь когда длина блока равна бесконечности. Но это скорее математическая мутота, не имеющая практической ценности.
Upd.
Хотя есть ещё третий вариант непрерывного спектра "в жизненных ситуациях". Когда разные сигналы накладываются друг на друга. Даже если один из них является идеальным с прерывным спектром, то другие могут быть с непрерывным. В данном случае переоцифровка (в пределе) сигнала ситуацию не разрулит, т.к. предел ограничен "вредным" сигналом. Эта ситуация вообще чаще всего бывает. Идеальный ЦОС-овик понимая все нюансы всех этапов прохождения своего сигнала будет просто приближаться к мат.пределу точности при правильном использовании инструментов. Правильно понимая достоверность результата при этом.
Upd2
Я бы с удовольствием замутил разговор страниц на 50 на эту тему. Только съезжу в отпуск на Бора-Бора
ДПФ/БПФ всего лишь свёртка с синусом aka интеграл.
ДПФ это не свёртка. ДПФ это умножение сигнала на матрицу, которая свёрткой не является.
Ну а если мы зануляем часть функции, то с чего бы это результат интеграла функции не изменится?
Дополнение сигнала нулями — это отнюдь не зануление части сигнала. Представьте, что у вас есть сигнал длины 512 точек и его копия, дополненная нулями до 1024 точек. ДПФ от второго сигнала будет совпадать с ДПФ от первого на сетке частот первого ДПФ. В этом смысле спектр не искажается. Но у второго ДПФ будет информация о сигнале на промежуточных частотах — результаты скалярных произведений с промежуточными частотами. Именно это я и называю полезными деталями. В случае, например, синусоидального сигнала эти промежуточные частотные отсчёты позволят вам более точно узнать частоту сигнала. А в случае фильтра — получить его АЧХ (которая, как известно, является непрерывной функцией частоты) в промежуточных точках по частоте, найти нули АЧХ и т.п.
В ДПФ/БПФ в конце идёт нормировка результата и она расчитана на 2^n, допустим 512 точек. Синус исходника был на интервале 500 точек.
Если дополнение нулями не кратное, то полученный спектр будет дискретной выборкой из непрерывного спектра исследуемого отрезка сигнала. Это может быть плохо или хорошо, в зависимости от задач. Чаще всего это хорошо, по тем же причинам, которые описаны выше: частотное разрешение анализа получается выше.
Гораздо серьёзней, когда блоки дополняются нулями и из них выцепляются низшие гармоники. Тут уже идут значительные фазовые искажения в дополнение к амплитудным.
Что-то не понял мысли...
ИМХО, непрерывный спектр существует только у частотно-модулированных сигналов или недооцифрованных.
И этой тоже...
ДПФ это не свёртка. ДПФ это умножение сигнала на матрицу, которая свёрткой не является.
ДПФ это свёртка с синусом и косинусом. И интеграл само собой.
Дополнение сигнала нулями — это отнюдь не зануление части сигнала. Представьте...
Я не писал зануление части сигнала. Не надо меня искажать. Если функция ФФТ юзает 512 точек, из которых 500 присутствуют, остальные нулевые, то это есть зануление части функции. Равноценно тому, что было получено 512 действительных точек, а потом 12 было занулено. Эквивалентно потери части информации в функции 512 точек. Однако львиная доля информации ещё осталось. Результат, относительно случая с полным набором точек будет искажён. Насколько велики искажения - (0.01%...ХХ%) зависит от многих нюансов. Часть я описал.
Если что-то непоняли, бывает. Это неудивительно, т.к. в книжках многое не пишут чтобы не перегружать читателя и/или не вызывать у читателя какие-то сомнения. Но если понимаете "физику процесса", то сразу понимаете море подводных камней, причём там, где никто никаких сомнений в книжках не высказывал.
Цитата
Alexey Lukin:
ДПФ это не свёртка. ДПФ это умножение сигнала на матрицу, которая свёрткой не является.
ДПФ это не свёртка. ДПФ это умножение сигнала на матрицу, которая свёрткой не является.
Вообще-то ДПФ можно представить и так и эдак. Например БПФ винограда основан на представлении дпф как свертки и вычислении длинной свертки через короткие.
Цитата
GetSmart:
в книжках многое не пишут чтобы не перегружать читателя и/или не вызывать у читателя какие-то сомнения.Но если понимаете "физику процесса", то сразу понимаете море подводных камней, причём там, где никто никаких сомнений в книжках не высказывал.
в книжках многое не пишут чтобы не перегружать читателя и/или не вызывать у читателя какие-то сомнения.Но если понимаете "физику процесса", то сразу понимаете море подводных камней, причём там, где никто никаких сомнений в книжках не высказывал.
Да нормально все в книжках пишут. Просто некоторые гурукиллеры читают их через 3 строки, а потом начинают с энтузиазмом преодолевать подводные камни.
Alexey Lukin, я кажется понял ваше непонимание процесса. Вы бы раскопали любой исходник ДПФ (не математическую формулу учебника, а код) особенно когда вычисляются не все гармоники, а только часть, что есть именно ДПФ, а не БПФ. И там очевидно, что гармоника идёт через нормированный интеграл. И если у входных данных функции (точнее у данных, принадлежащих гармонике) часть данных нулевая, то интеграл будет иметь меньшее значение, чем у полных данных. А соответственно и окончательный результат. То, что все другие способы вычисления ДПФ дают аналогичный результат, я почти уверен. Видимо когда ДПФ кажется умножением на матрицу, то в этом процессе волшебным способом всё решается и понимать не надо. А от дополнения нулями результат становится всё лучше и лучше 
Где логика? 20 постов почти все утверждают, что от дополнения нулями результат не хуже. Это я так книжки читаю или это другие нахватались знаний не из книжек. Я зашёл чтобы поправить чужие заблуждения. И это моё мнение о том почему так происходит. Если бы в учебниках/книгах все нюансы/подводные камни были бы хотя бы обозначены, то таких глюков в рассуждениях было бы значительно меньше.
Upd.
Ещё более наглядное объяснение. ДПФ/БПФ в качестве результата даёт амплитуду/фазу гармоники интегрально за весь блок. Если в блоке 1/3 данных обнулена, то ессно интегральное значение амплитуды будет меньше на 1/3. Но ещё фишка в том, что это обнуление порождает "запредельные" гармоники, которых в исходном сигнале не должно было быть, то есть с частотой больше Fd/2 и меньше 1/Т. Именно они будут портить качество/достоверность результата уже в таком виде, что простая перенормировка не поможет.
Цитата(thermit)
Да нормально все в книжках пишут. Просто некоторые гурукиллеры читают их через 3 строки, а потом начинают с энтузиазмом преодолевать подводные камни.
Где логика? 20 постов почти все утверждают, что от дополнения нулями результат не хуже. Это я так книжки читаю или это другие нахватались знаний не из книжек. Я зашёл чтобы поправить чужие заблуждения. И это моё мнение о том почему так происходит. Если бы в учебниках/книгах все нюансы/подводные камни были бы хотя бы обозначены, то таких глюков в рассуждениях было бы значительно меньше.
Upd.
Ещё более наглядное объяснение. ДПФ/БПФ в качестве результата даёт амплитуду/фазу гармоники интегрально за весь блок. Если в блоке 1/3 данных обнулена, то ессно интегральное значение амплитуды будет меньше на 1/3. Но ещё фишка в том, что это обнуление порождает "запредельные" гармоники, которых в исходном сигнале не должно было быть, то есть с частотой больше Fd/2 и меньше 1/Т. Именно они будут портить качество/достоверность результата уже в таком виде, что простая перенормировка не поможет.
ДПФ это свёртка с синусом и косинусом. И интеграл само собой.
Повторю ещё раз: ДПФ это не свёртка. Откуда вы это взяли? Цитату из книжки привести можете? Вы могли прочитать, что "скользящее ДПФ — это набор свёрток". Могли прочитать, что "ДПФ можно выразить (вычислить) через свёртку". Но говорить, что "ДПФ это свёртка" — всё равно, что говорить, что "число пи — это сумма бесконечного ряда". Конечно, число пи можно вычислисть как сумму ряда, но это отнюдь не определение. Прежде чем укорять меня в невнимательном чтении книжек лучше сами с ними разберитесь для начала...
Я не писал зануление части сигнала. Не надо меня искажать.
Писали, и до сих пор пишете. Мы с вами просто с разных позиций говорим: вы считаете, что сигнал из 512 точек у вас был, а я считаю, что его никогда не было, а было только 500. Спорить бесполезно.
Вообще-то ДПФ можно представить и так и эдак. Например БПФ винограда основан на представлении дпф как свертки и вычислении длинной свертки через короткие.
Как я уже написал выше, представить-то можно, только это не есть определение. И в этом представлении сворачивается не исходный сигнал с синусами и косинусами, как пишет GetSmart, а другие сигналы.
Alexey Lukin, я кажется понял ваше непонимание процесса. Вы бы раскопали любой исходник ДПФ (не математическую формулу учебника, а код) особенно когда вычисляются не все гармоники, а только часть, что есть именно ДПФ, а не БПФ. И там очевидно, что гармоника идёт через нормированный интеграл. И если у входных данных функции (точнее у данных, принадлежащих гармонике) часть данных нулевая, то интеграл будет иметь меньшее значение, чем у полных данных. А соответственно и окончательный результат.
Вообще-то я неплохо знаком с исходниками ДПФ
Слово "спектр" имеет множество значений, и одно из них — это результат ДПФ. Вы не согласны? Словосочетание "комплексный спектр" вам незнакомо?
Прежде чем укорять меня в невнимательном чтении книжек лучше сами с ними разберитесь для начала...
Взял уже любой исходник кода и разобрался. Или это непонимание из серии теоретика с практиком? Мне например гораздо важнее что практически происходит с дискретным сигналом, а не теоретически (точнее должно происходить). Теоретики любят черезмерно упрощать свои входные данные и особенно идеальность преобразований. А так же сувать везде бесконечность. Всё это особенно когда учат других. Как пример первые 5 постов здесь. Ну никто не догадался сказать о мало того что искажении амплитуды, но и о искажениях младших гармоник. Хотя какие гармоники ТС интересовали было не ясно, а значит вполне вероятно и младшие тоже.
Цитата
Писали, и до сих пор пишете. Мы с вами просто с разных позиций говорим: вы считаете, что сигнал из 512 точек у вас был, а я считаю, что его никогда не было, а было только 500. Спорить бесполезно.
Вам видней, полезно или нет. Однако я считаю что был сигнал 500 точек, но в функцию, требующую 512 точек засунули 500, остальные нули. То есть не что-то там было где-то, а аргумент функции (который должен быть информативным) частично занулили. Дальше не повторяю.
Цитата
Как я уже написал выше, представить-то можно, только это не есть определение. И в этом представлении сворачивается не исходный сигнал с синусами и косинусами, как пишет GetSmart, а другие сигналы.
В данном случае определений можно дать множество одного и того же сложного действия. Хотя любопытно к какому определению апеллируете вы. (слово интересное - даже гугл не понял как правильно писать - аппелируете или апеллируете
Цитата
И даже защитил диссертацию практически по спектральному анализу. Вы мне пытаетесь толковать про какую-то тривиальщину: нормировку коэффициентов, "интегралы", "запредельные гармоники"... А я вам про практический результат о форме спектра.
Серьёзно? А по постам и не скажешь
Наверное суровые профессионалы считают, что тривиальщина вообще не стоит упоминания. И такие же профи пишут учебники.
Судя по этому
Цитата
Чем больше добавляется нулей, тем точнее получается спектр сигнала. Конечно, это тот же самый спектр, но на более плотной сетке частот
Диссертации там, где вы защищали, принимают неглядя.
PS
Если вас не затруднит, то расскажите поподробней это
Цитата
Ничего не искажается! Наоборот, становится видно больше правильных деталей
"Правильные детали" заинтриговали
Вам видней, полезно или нет. Однако я считаю что был сигнал 500 точек, но в функцию, требующую 512 точек засунули 500, остальные нули. То есть не что-то там было где-то, а аргумент функции (который должен быть информативным) частично занулили. Дальше не повторяю.
Ок, мы пришли к согласию в этом вопросе.
В данном случае определений можно дать множество одного и того же сложного действия. Хотя любопытно к какому определению аппелируете вы.
Да какое там сложное действие... Вот определение, другого просто не бывает:

Как видите, ни свёртки, ни интегралов в нём нет. Есть набор скалярных произведений — проекция вектора на другой базис (либо умножение на матрицу, что то же самое).
Если вас не затруднит, то расскажите поподробней это
"Правильные детали" заинтриговали
"Правильные детали" заинтриговали
Я уже написал выше более подробно: "В случае, например, синусоидального сигнала эти промежуточные частотные отсчёты позволят вам более точно узнать частоту сигнала. А в случае фильтра — получить его АЧХ (которая, как известно, является непрерывной функцией частоты) в промежуточных точках по частоте, найти нули АЧХ".
Разве это не "полезные, правильные детали"?
Вот определение, другого просто не бывает:

Как видите, ни свёртки, ни интегралов в нём нет. Есть набор скалярных произведений — проекция вектора на другой базис (либо умножение на матрицу, что то же самое).

Как видите, ни свёртки, ни интегралов в нём нет. Есть набор скалярных произведений — проекция вектора на другой базис (либо умножение на матрицу, что то же самое).
Хотел было попросить привести определение свёртки, но... сэкономлю время.
Сумма и интеграл = аналоги, только сумма применяется в ограниченном множестве, точнее просто во множестве, но обычно в ограниченном. Так что сумма aka интеграл уже есть.
Свёртка - это сумма/интеграл произведения функций. А в данном случае функция = комплексный синус (или как там он по фен-шую называется?
Upd.
В дополнение к интегралу: в зависимости от типа ПФ в "определении" (хотя по-моему это называется формулой) будет либо интеграл, либо сумма. Но "физика процесса" одна и та же.
В дополнение к свёртке: можно считать комплексный синус aka формулу Эйлера ядром узкополосного фильтра. То есть свёртка происходит с ядром фильтра. И на выходе имеем отфильтрованную одну гармонику.
Дальнейший спор мне представляется бессмысленным. Прежде чем спорить, неплохо бы разобраться с простейшими понятиями: комплексный синус и комплексная экспонента, сумма и интеграл, свёртка и ДПФ, "запредельные гармоники" и боковые лепестки. А то получается, как в рассказе Шукшина "Срезал"...
Чтобы проиллюстрировать полезные детали спектра, открывающиеся при дополнении сигнала нулями, специально для вас (и других читателей форума) приготовил иллюстрации. На первой — синусоида с частотой 1 кГц. Спектр без дополнения нулями не позволяет даже толком определить её частоту. При дополнении нулями не только проявляется частота в 1 кГц, но и становятся отчётливо видны боковые лепестки окна.
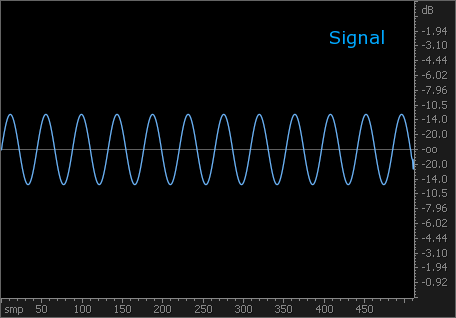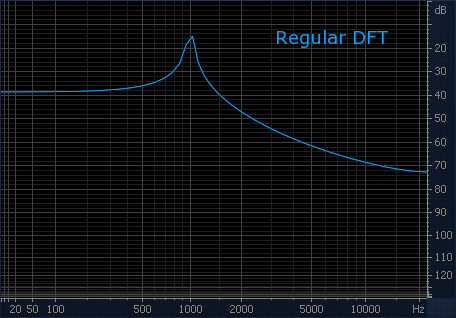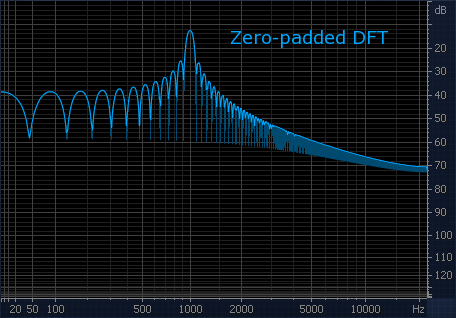
На второй — ядро НЧ-фильтра. Спектр без дополнения нулями производит замечательное (но неверное!) впечатление об АЧХ фильтра. При дополнении нулями проявляется наличие значительных пульсаций, как в полосе пропускания, так и в полосе подавления. Становятся также видны нули фильтра. Это и есть реальная АЧХ.
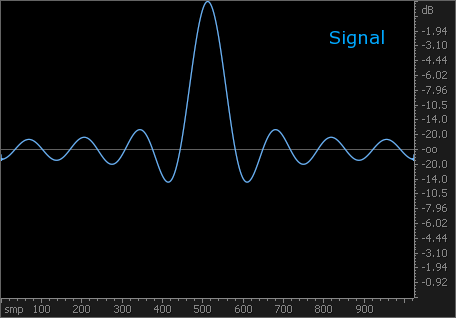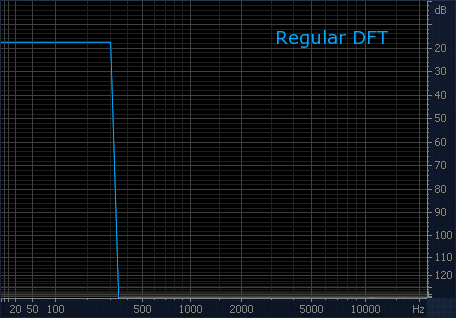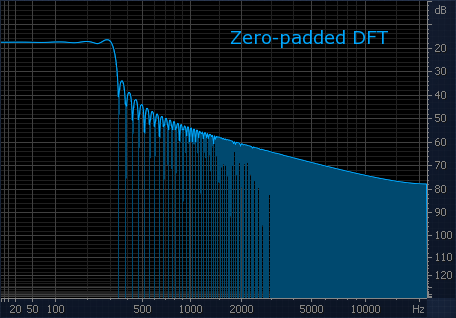
Чтобы проиллюстрировать полезные детали спектра, открывающиеся при дополнении сигнала нулями, специально для вас (и других читателей форума) приготовил иллюстрации. На первой — синусоида с частотой 1 кГц. Спектр без дополнения нулями не позволяет даже толком определить её частоту. При дополнении нулями не только проявляется частота в 1 кГц, но и становятся отчётливо видны боковые лепестки окна.

На второй — ядро НЧ-фильтра. Спектр без дополнения нулями производит замечательное (но неверное!) впечатление об АЧХ фильтра. При дополнении нулями проявляется наличие значительных пульсаций, как в полосе пропускания, так и в полосе подавления. Становятся также видны нули фильтра. Это и есть реальная АЧХ.

Дальнейший спор мне представляется бессмысленным.
Вот тут я пожалуй соглашусь.
Спорить с человеком, который не понимает что и почему у него отображается на графиках наверно бесполезно.
Блажен кто верует, что спектр чистого синуса имеет вид как на первой картинке. Однако прикольно осознавать, что не меняя синал, но слегка меняя условия оцифровки спектр одного и того же сигнала будет заметно меняться. Это явно чудо, т.к. как утверждал Котельников, соблюдая условие верхней частоты оцифровки сигнал, после дискретизации во времени, представляется без потери информации. При этом линейное его фурье-преобразование почему-то может давать разные спектры.
PS. Спектр - это не одна самая высокая палка. Спектр это полный набор гармоник.
PPS. Если хотите поточнее увидеть спектр своего синуса - используйте оконную функцию. Только не говорите, что результат будет менее достоверный. Ну а потом сравните со своим на первой картинке. И потом уже можно приступать к обсуждению "полезных, правильных деталей".
Слово "спектр" имеет множество значений, и одно из них — это результат ДПФ. Вы не согласны? Словосочетание "комплексный спектр" вам незнакомо?
Слово спектр имеет действительно множество трактовок, но в радиотехническом смысле только одну. Есть совершенно четкое определение спектра в радиотехнике. дпф определено для периодических дискретных последовательностей с периодом равным размеру дпф. т е только для периодического сигнала с периодом равным размеру дпф отсчеты дпф будут совпадать с отсчетами спектра на частотах кратных бину. Во всех остальных случаях - нет. Собственно, все растекания, и другие подводные камни возникают от игнорирования этого несложного факта. Кандидатам наук, вероятно, такие толстые тонкости побарабану...
thermit, вы не томите, подскажите ваше определение спектра. Я догадываюсь, что вы говорите о спектральной плотности энергии, но хочу, чтобы вы сами это сказали, а заодно — рассказали, как его (её) вычислить.
inf
S(w)=SUM( x(n) * exp(-j*w*n) )
n=-inf
Спектр дискретного сигнала.
Кто такая спектральная плотность энергии -
не в курсе.
Щас скажу умную вещь 
Спектры бывают разные. Поэтому вопросы нужно задавать корректно. И понимать, что просто (сокращенно) термин спектр выражает всё общее, что есть в разных подвидах спектров. А это - функция амплитуды и фазы по частоте. А уж непрерывная это функция или множество и прочие нюансы выражаются в контексте слова спектр. Дисретный, непрерывный и прочие.
Ну и докучи, в непрерывном сигнале спектр всегда достоверней чем в дискретном. Даже в одинаковом периоде, хотя бы потому, что выборок в непрерывном сигнале = бесконечность.
Спектры бывают разные. Поэтому вопросы нужно задавать корректно. И понимать, что просто (сокращенно) термин спектр выражает всё общее, что есть в разных подвидах спектров. А это - функция амплитуды и фазы по частоте. А уж непрерывная это функция или множество и прочие нюансы выражаются в контексте слова спектр. Дисретный, непрерывный и прочие.
Ну и докучи, в непрерывном сигнале спектр всегда достоверней чем в дискретном. Даже в одинаковом периоде, хотя бы потому, что выборок в непрерывном сигнале = бесконечность.
О! Наконец-то Гуру-киллер сказал умную вещь! 
У меня даже появилось желание ответить вам про весовые окна. Моё весовое окно прямоугольное, но в данном случае это не меняет вывода о пользе дополнения нулями. С другим весовым окном будет то же самое: от дополнения нулями и частота станет видна точнее, и боковые лепестки окна.
Согласен, но это для бесконечного сигнала. Разве такие бывают на практике? Да и если в формулу подставить бесконечную синусоиду, сумма разойдётся.
Я согласен с трактовкой Гуру-киллера: спектр — это общее понятие, они бывают разных видов в зависимости от ситуации и от вида анализа сигнала. Кстати, Википедия тоже так считает.
У меня даже появилось желание ответить вам про весовые окна. Моё весовое окно прямоугольное, но в данном случае это не меняет вывода о пользе дополнения нулями. С другим весовым окном будет то же самое: от дополнения нулями и частота станет видна точнее, и боковые лепестки окна.
inf
S(w)=SUM( x(n) * exp(-j*w*n) )
n=-inf
Спектр дискретного сигнала.
S(w)=SUM( x(n) * exp(-j*w*n) )
n=-inf
Спектр дискретного сигнала.
Согласен, но это для бесконечного сигнала. Разве такие бывают на практике? Да и если в формулу подставить бесконечную синусоиду, сумма разойдётся.
Я согласен с трактовкой Гуру-киллера: спектр — это общее понятие, они бывают разных видов в зависимости от ситуации и от вида анализа сигнала. Кстати, Википедия тоже так считает.
Тогда скажу ещё одну умную вещь. Можно не хлопать 
Нужно всегда понимать и указывать спектр чего (а не только какой) имеется ввиду. Если говорить о спектре чистой синусоиды, то есть "исходника" даже на ограниченном интервале, то у неё будет чистый спектр в виде одной дельта-функции. В идеальном дискретном представлении это была бы "палка" aka бин с честной амплитудой/фазой. Так что кто бы что тут не "втирал" но "честный" спектр исходника-синуса должен быть "палкой", то бишь все остальные "палки" должны быть нулевые. А вот все остальное на реальном спектре - это искажения в представлении "исходника". Но искажения возникают не в самом процессе дискретизации, а в использовании определённого мат.аппарата и определённых отношений параметров самого сигнала и ограниченности данных, использованных в мат.аппарате.
Нужно всегда понимать и указывать спектр чего (а не только какой) имеется ввиду. Если говорить о спектре чистой синусоиды, то есть "исходника" даже на ограниченном интервале, то у неё будет чистый спектр в виде одной дельта-функции. В идеальном дискретном представлении это была бы "палка" aka бин с честной амплитудой/фазой. Так что кто бы что тут не "втирал" но "честный" спектр исходника-синуса должен быть "палкой", то бишь все остальные "палки" должны быть нулевые. А вот все остальное на реальном спектре - это искажения в представлении "исходника". Но искажения возникают не в самом процессе дискретизации, а в использовании определённого мат.аппарата и определённых отношений параметров самого сигнала и ограниченности данных, использованных в мат.аппарате.
Сомневающимся, что дополнение нулями улучшает представление спектра (не увеличивает разрешение по частоте, а просто показывает больше точек в том же спектре), посмотрите Р. Лайонс. Цифровая обработка сигналов, рис 3.21. Поначалу удивляет, это да... 
для Alexey Lukin
по первой картинке хочу спросить - сколько точек было ДПФ до заполнения нулями и после - 512 и ...?
Насчет свертки - свертка принимает две последовательности во временной области и выдает результат во временной области. Еще бывает и в частотной, но тоже - и входы, и выходы.
P.S. было бы неплохо, чтобы не только GetSmart дополнял и поправлял fontp, но и наоборот.
для Alexey Lukin
по первой картинке хочу спросить - сколько точек было ДПФ до заполнения нулями и после - 512 и ...?
Насчет свертки - свертка принимает две последовательности во временной области и выдает результат во временной области. Еще бывает и в частотной, но тоже - и входы, и выходы.
P.S. было бы неплохо, чтобы не только GetSmart дополнял и поправлял fontp, но и наоборот.
А можно поближе к земным материям? я чет из всего вышесказанного ничего не понял! К своему сожалению А ответа на свой вопрос так и не получил. Теперь когда уже все обсудили,пришли к общим определениям, можно немного практики. Все таки число отсчетов чему равно должно быть? Есть шаг дискретизации 40мкс. Есть частота силового напряжения 50Гц. Есть ДСП процессор, в котором аппаратно реализовано быстрое преобразование Фурье по основанию 2. Диапазон частот осциллографируемых гармонических сигналов 0-51Гц. Число отсчетов должно укладываться в целый период? Надо брать несколько периодов, или достаточно одного? как быть для низкочастотных сигналов например 20 Гц, если отсчеты например не уложились в период (массив 1024 элементов, а сигнал имеет 1250 дискрет), как это повлияет на дальнейший анализ сигнала? частота 20Гц будет иметь максимальный лепесток после разложения данного сигнала?
А ответа на свой вопрос так и не получил. Теперь когда уже все обсудили,пришли к общим определениям, можно немного практики. Все таки число отсчетов чему равно должно быть? Есть шаг дискретизации 40мкс. Есть частота силового напряжения 50Гц. Есть ДСП процессор, в котором аппаратно реализовано быстрое преобразование Фурье по основанию 2. Диапазон частот осциллографируемых гармонических сигналов 0-51Гц. Число отсчетов должно укладываться в целый период? Надо брать несколько периодов, или достаточно одного? как быть для низкочастотных сигналов например 20 Гц, если отсчеты например не уложились в период (массив 1024 элементов, а сигнал имеет 1250 дискрет), как это повлияет на дальнейший анализ сигнала? частота 20Гц будет иметь максимальный лепесток после разложения данного сигнала?
А можно поближе к земным материям?...
БПФ потому так называется, что количество выборок кратно степени 2 (ну, или 4, например).
Конечно, именно столько и нужно брать выборок. А то, что период сигнала не уложится ровненько в этот массив, так для этого существуют окна, которые больше или меньше давят края этого массива.
А вы книжку скачайте, что я выше упомянул. Она имеется на просторах интернет (и здесь, рядом, тоже была...) . Там всё просто и красиво изложено.
Мне нравится как дискуссия по поводу спектра (в большинстве случаев) плавно уходит в метафизику =)
Немного отсебятенки к определению спектра:
Основополагающим стержнем держащим все здание под названием "спектр, спектральный анализ" является понятие о гармонической природе всех сигналов, т.е. "вера" (именно вера) в то, что у "чистого" синуса спектр бесконечно узкий (одна палка) и только эта "вера" позволяет нам утверждать что любой сигнал можно разложить в ряды Фурье (как правило оговаривается то, что сигнал должен быть "гармоническим", чтобы все было чисто с юридической точки зрения), а соответственно и вычислить спектр.
Ну а теперь если подумать, существуют ли гармонические сигналы? Конечно же нет, это сугубо математическая абстракция, ведь невозможно эмпирически доказать обратное (АЦП с частотой дискретизации бесконечность никогда не будет создан). Тем самым осуществляя преобразование Фурье мы самолично принимаем решение о входе в мир абстракций и уходе от "реальности". Вроде, пока что, ныне существующего понятия о сигналах вполне достаточно для реальных задач.
Могу ошибаться конечно же=)
Немного отсебятенки к определению спектра:
Основополагающим стержнем держащим все здание под названием "спектр, спектральный анализ" является понятие о гармонической природе всех сигналов, т.е. "вера" (именно вера) в то, что у "чистого" синуса спектр бесконечно узкий (одна палка) и только эта "вера" позволяет нам утверждать что любой сигнал можно разложить в ряды Фурье (как правило оговаривается то, что сигнал должен быть "гармоническим", чтобы все было чисто с юридической точки зрения), а соответственно и вычислить спектр.
Ну а теперь если подумать, существуют ли гармонические сигналы? Конечно же нет, это сугубо математическая абстракция, ведь невозможно эмпирически доказать обратное (АЦП с частотой дискретизации бесконечность никогда не будет создан). Тем самым осуществляя преобразование Фурье мы самолично принимаем решение о входе в мир абстракций и уходе от "реальности". Вроде, пока что, ныне существующего понятия о сигналах вполне достаточно для реальных задач.
Могу ошибаться конечно же=)
Мне нравится как дискуссия по поводу спектра (в большинстве случаев) плавно уходит в метафизику =)
...
Ну а теперь если подумать, существуют ли гармонические сигналы?
...
Могу ошибаться конечно же=)
...
Ну а теперь если подумать, существуют ли гармонические сигналы?
...
Могу ошибаться конечно же=)
Ничего страшного, если мы пытаемся дойти собственными размышлениями до понимания. Даже, наоборот.
Но в данном случае спектр - абсолютно точное математическое преобразование. Естественно, в реальности это преобразование можно осуществить с какой-то заданной точностью (хотя бы, разрядностью чисел ограничено). Но только и всего. Для сигнала, преобразованного в цифровую форму, появляются неточности, связанные с частотой дискретизации, количеством отсчетов в реализации, разрядностью АЦП, линейностью АЦП, джиттером частоты дискретизации, шумом.
Про гармонические сигналы. Если сигнал гармонический, т.е. содержит всего одну синусоидальную составляющую, то и спектр его - одна палка. Это, так сказать, разными словами говорится об одном. А если взять, например, прямоугольный сигнал, то в спектре у него - куча гармоник. Но вычислить его спектр тоже можно со сколь угодно большой точностью.
Синус - это не от балды взятый сигнал. Возьмите колесо, поставьте его в центр координатных осей X и Y, задайте на ободе колеса точку, и крутите это колесо с равномерной скоростью. И посмотрите, как изменяются координаты этой точки по Х и Y со временем.
И много в природе движется так, равномерно вращаясь. С определенной долей допущения, конечно.
Ничего страшного, если мы пытаемся дойти собственными размышлениями до понимания. Даже, наоборот.
Я не в коем случае никого не обвиняю в не компетентности, дискуссию выше прочитал с удовольствием. Я просто в очередной раз подмечаю, что основы радиотехники имеют под собой достаточно хлипкий фундамент (и не я один). С другой стороны из этого хлипкого вырисовываются достаточно крепкие математические модели. Мое замечание, что все клонится к метафизике это не насмешка, я и в правду думаю что тут надо копать в сторону "А как же математика завязана с реальностью?", чтобы хоть чуть чуть взбодрить теорию о спектре, рядах фурье и прочем.
Но в данном случае спектр - абсолютно точное математическое преобразование. Естественно, в реальности это преобразование можно осуществить с какой-то заданной точностью (хотя бы, разрядностью чисел ограничено). Но только и всего. Для сигнала, преобразованного в цифровую форму, появляются неточности, связанные с частотой дискретизации, количеством отсчетов в реализации, разрядностью АЦП, линейностью АЦП, джиттером частоты дискретизации, шумом.
Угумс, спектр это математическая "фича", позволяющая объединить эмпирический опыт тысячи исследователей с учетом джиттера/разрядности/ и прочего. Т.е. в моем понимание понятие спектра это инструмент, а не объяснение.
Про гармонические сигналы. Если сигнал гармонический, т.е. содержит всего одну синусоидальную составляющую, то и спектр его - одна палка. Это, так сказать, разными словами говорится об одном. А если взять, например, прямоугольный сигнал, то в спектре у него - куча гармоник. Но вычислить его спектр тоже можно со сколь угодно большой точностью.
Синус - это не от балды взятый сигнал. Возьмите колесо, поставьте его в центр координатных осей X и Y, задайте на ободе колеса точку, и крутите это колесо с равномерной скоростью. И посмотрите, как изменяются координаты этой точки по Х и Y со временем.
И много в природе движется так, равномерно вращаясь. С определенной долей допущения, конечно.
Синус - это не от балды взятый сигнал. Возьмите колесо, поставьте его в центр координатных осей X и Y, задайте на ободе колеса точку, и крутите это колесо с равномерной скоростью. И посмотрите, как изменяются координаты этой точки по Х и Y со временем.
И много в природе движется так, равномерно вращаясь. С определенной долей допущения, конечно.
Я вот не могу догнать почему именно так, почему именно синус? Моск разрывается просто =)
Есть у Юнга достаточно интересное произведение - Синхроничность называется, то же моск взрывает.
Я вот не могу догнать почему именно так, почему именно синус? Моск разрывается просто =)
Колесо. Если хотите, покрутите на веревке шарик, и посмотрите сбоку.
Это всё оттого, что всё в мире вращается, от электронов до галактик.
Вот и вся метафизика.
Колесо. Если хотите, покрутите на веревке шарик, и посмотрите сбоку.  Или - как меняется продолжительность дня от времени года.
Или - как меняется продолжительность дня от времени года.
Это всё оттого, что всё в мире вращается, от электронов до галактик.
Это всё оттого, что всё в мире вращается, от электронов до галактик.
То то и оно, что доказательство (а точнее объяснение) понятия спектра/гармонии и прочего является примеры Вами приведенные=)
Для просмотра полной версии этой страницы, пожалуйста, пройдите по ссылке.
